| Air traffic control requires that the routes of aircraft be restricted. We want
to investigate the costs of requiring aircraft to fly only in a few directions.
For example, we could require them to fly only north, east, south, or west.
It makes sense to distribute the allowable directions evenly. If we allow only
n directions, one will be east and the others will be evenly distributed among
all other possible directions. So if n is 3, the three directions are east, 30 degrees
west of north, and 30 degrees west of south. Adjacent directions then differ
by 120 degrees. Notice that if a direction is legal the opposite direction
may not necessarily be legal.
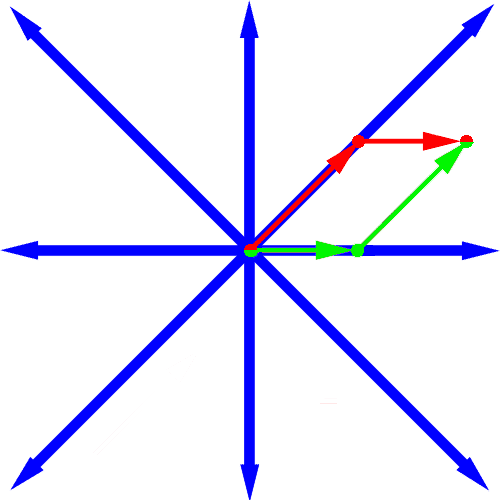
The following picture shows a minimum way to fly to a destination which is 5 east and 3 north of the starting point when n is 8. The 8 allowable directions are shown in blue.
By flying a distance of 3*sqrt(2) northeast, and then 2 east (or 2 east, and then 3*sqrt(2) northeast) we can get to our
destination by travelling a total distance of 3*sqrt(2) + 2. Notice that for any n and destination
the minimal distance can be achieved using no more than two directions.
Create a class Airways that contains a method distance that is given n (the number
of legal directions), east (the distance eastward to our destination), and north (the
distance northward to our destination). It returns the minimum distance we will have
to fly to get to our destination under these requirements.
| 