Some square tiles have been selected from a N x M chessboard,
building a pattern (not necessarily connected). You have the task of coloring
some of the selected tiles red and all of the others blue so that the pattern
composed by the blue tiles is a shifted copy of the
pattern composed by the red tiles.
One example is shown in the figure below (the white tiles in the left
image are the selected tiles, which are colored in the right image).
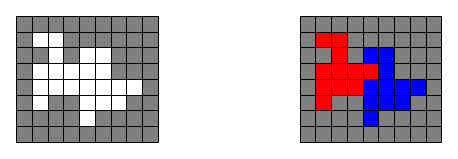
You will be given a String[] board containing N
elements, each of them M characters long, with a character '#'
indicating that the tile in the corresponding position belongs to the
selected tiles (i.e., to be colored, the white tiles in the example
above), a character '.' indicating a tile that shall be ignored
(the gray tiles in the example above).
Return a String[] representing the red pattern,
after
cropping the image to the smallest rectangle that contains all the red tiles.
Use the character '#' to denote tiles painted in red, '.' to denote other
tiles. If there are several ways to color the tiles so that two
equal patterns are created (one in red, one in blue), use the solution
in which the red pattern has the smallest width (horizontal
distance from the leftmost red tile to the rightmost red tile). If there
are several ways with the smallest width, use the solution among them
with the smallest height (vertical distance from the uppermost red tile
to the lowermost red tile).
If there is still a tie, use the one among the tied ones that comes first
lexicographically after you concatenate the Strings representing
the solution ('#' comes before '.').
If there is no solution, return an empty String[].
| 