You are given a rows x cols chessboard, and a cuboid
with dimensions 1 x 1 x 3 standing on its small side (1 x 1) on
one of the squares of the chessboard. You are trying to move the cuboid
to another square, by tilting the cuboid over one of its base sides
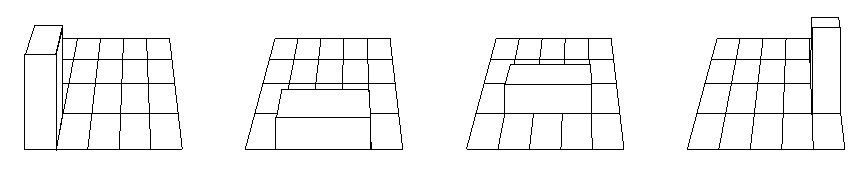
to some neighboring squares. The example figure below shows a
1 x 1 x 3 cuboid standing on the lower left square (first image).
After the first move it lies on its 1 x 3 side in the middle of the
lowest row (second image). After the second move it lies on
its 1 x 3 side in the middle of the second lowest row. Finally, after the
third move it is standing on its 1 x 1 side on the rightmost square of the
second lowest row.
You are given rows and cols, specifying the number of
rows and columns of the board.
Further, you are given a int[] start and a
int[] target, specifying the beginning and
target positions of the cuboid, respectively. Both
start and target will have exactly two elements.
The first specifies the row and the second the column of the position
(both 0-based). At the beginning,
the cuboid is standing on its 1 x 1 side on the square specified
by start. You are to return the minimum number of moves needed to
move the cuboid so that it is standing on its 1 x 1 side on the square
specified by target. During movement of the cuboid, no part
of it may ever be outside the board limits specified by
rows and cols. If the cuboid can not be moved
to the target position, return -1. If the cuboid already is at
the target square at the beginning, return 0.
| 