Problem Statement |
| | Consider a group of metal springs supporting a rigid rod.
The rod's weight is
uniformly distributed along its length at a rate of 1 pound per inch. Each of
the springs exerts an upwards force when it is compressed. This force is given
by Fi = ki*xi+1/(maxi-xi)2 where Fi is the force, xi is the amount the spring
is compressed (xi may be negative, in which case the spring is extended and the
force may be downward), and maxi and ki are inputs. Notice that as the compression approaches max, the force goes to infinity, so the spring will never be compressed by max or more. Given the positions, k's, and max's for the springs supporting the rod (corresponding elements of the inputs represent one spring), you are to determine how much each
spring is compressed by the rod. You may assume that the leftmost spring
supports the leftmost end of the rod, while the rightmost spring supports the
rightmost end of the rod. Note that some of the springs may be negatively
compressed (see examples).
There are three basic conditions that must be fulfilled by the compressions of
the springs. First, the total force exerted upwards (the sum of the F's) must
equal the weight of the rod. Second, since the rod is rigid, the compressions
of the springs must be such that the tops of the springs are all in a line (with
some constant slope). Third, the sum of the torques around every point where
the rod touches a spring must be 0. The torques come from both the upward (or downward)
forces exerted by the springs, and also from the weight of the rod. The torque
around a point due to a spring is equal to the force exerted by the spring times
the horizontal distance from the spring to the point. The torque around a point caused by
the weight of the rod to the right of the point is equal to the weight of the portion of the rod to the right squared, and then divided by 2. The left side of the point is analogous. See examples for more information.
|
| |
Definition |
| | | Class: | Springs | | Method: | compression | | Parameters: | int[], int[], int[] | | Returns: | double[] | | Method signature: | double[] compression(int[] positions, int[] ks, int[] maxs) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | In reality, the rotation of the rod would result in some more complicated effects which we will ignore for this problem. |
| - | When none of the springs are compressed at all, their tops form a horizontal line. |
| |
Constraints |
| - | positions, ks and maxs will each contain between 2 and 50 elements, inclusive. |
| - | positions, ks and maxs will each contain the same number of elements. |
| - | positions will be sorted in strictly ascending order. |
| - | Each element of positions will be between 0 and 1000, inclusive. |
| - | Each element of maxs and ks will be between 1 and 1000, inclusive. |
| |
Examples |
| 0) | |
| | {0,1,3}
| {1,1,1}
| {1000,1000,1000} |
| Returns: {0.857141855426, 0.964284712354, 1.17857042621 } | 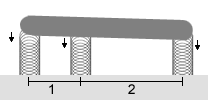
The image above shows the approximate setup of the springs and rod. The values in maxs are large enough that we can ignore them in this discussion and our results won't be far off. The first spring is compressed by 6/7, the second by 27/28, and the third by 33/28. You will note that the sum of these three compressions is 3. Furthermore, the slope of the rod (3/28) matches the compression of the springs. Finally, we can calculate the torque at each location (negative values indicate counterclockwise torque):
Torque due to:
Position | Spring 0 | Spring 1 | Spring 2 | Weight of Left | Weight of Right
---------+----------+----------+----------+----------------+----------------
0 | 0 | -27/28*1 | -33/28*3 | 0 | 3*3/2 = 9/2
1 | 6/7 * 1 | 0 | -33/28*2 | -1*1/2=-1/2 | 2*2/2 = 2
3 | 6/7 * 3 | 27/28*2 | 0 | -3*3/2=-9/2 | 0
You can easily verify that the sum of the torques at each of the three positions is 0.
When you solve the problem taking max into account, you find that each of the above values is approximately one millionth too high. |
|
|
| 1) | |
| | {0,1,2,4} | {2,1,1,1} | {1,10,10,10} |
| Returns: {0.066863594314, 0.421263093855, 0.775662593396, 1.484461592477 } | |
|
| 2) | |
| | {1,99,101} | {1,100,100} | {1000,1000,1000} |
| Returns: {48.510296857713, 0.744851008845, -0.229954008478 } | |
|
| 3) | |
| | | Returns: {0.955235859695, 0.499999998999 } | |
|
