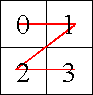
| | A Z-curve is a path that traces through all the points in a two-dimensional square grid in such a way that the four quadrants are visited in order: first the upper left, then the upper right, then the lower left, and finally the lower right. If those quadrants contain more than 1 cell, these cells are visited recursively, in the same manner. A Z-curve of order N is a path through a 2^N by 2^N grid. A Z-curve of order 1 is a simple Z-shape through a 2-by-2 grid, as shown below.
Here is a diagram of a Z-curve of order 2.
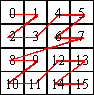
Notice the order each quadrant was visited:
- upper left quadrant: 0, 1, 2, 3
- upper right quadrant: 4, 5, 6, 7
- lower left quadrant: 8, 9, 10, 11
- lower right quadrant: 12, 13, 14, 15
You will be given a value N and coordinates r and c denoting the row and the column in a 2^N by 2^N grid. Coordinates range from 0 to (2^N)-1 inclusive, with the upper left corner at coordinates (0,0). Assuming you start from the upper left corner and the points are traversed in the order specified by a Z-curve of order N, determine how many steps it takes to reach the point at coordinates (r,c).
|


