TopCoder problem "ManhattanDistance" used in SRM 272 (Division I Level Three)



Problem Statement

    

We are in a Manhattan-type city with north-south directed avenues labeled "A" to "Z" and east-west directed streets numbered 1 to 50. A crossing is represented by the label of the avenue followed by the label of the street defining that crossing, with no leading zeros (e.g., the crossing between avenue "D" and street number 12 is represented as "D12").

The figure below shows part of the city (avenues E to G, streets 2 to 4). The distance between neighboring streets and between neighboring avenues will be the same for all pairs of neighboring avenues or streets, and will be given by the input parameter distance (in meters). This distance is measured from the center of the streets or avenues, as shown in the figure. Further, all streets and avenues will have the same width, which will be given by the input parameter width (also in meters), as shown in the figure.

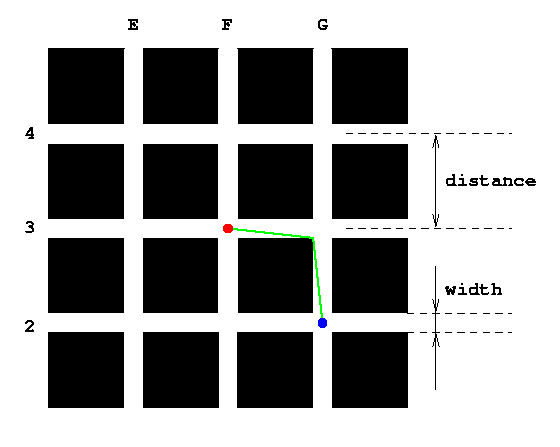
Given distance and width as defined above, as well as the representation of two crossings, start and target (formatted as described above), return the minimum distance you have to travel (in meters) beginning from the center of the crossing start to reach the center of the crossing target if you are only allowed to travel on streets and avenues. For example, if start is "F3" (the red dot in the figure above) and target is "G2" (the blue dot), the green line shows one possible optimal path to go from start to target (another optimal path with the same length would be to go first south to the north-east corner of crossing "F2" and then to the east to our target).

 

Definition

    
Class:ManhattanDistance
Method:minDistance
Parameters:int, int, String, String
Returns:double
Method signature:double minDistance(int distance, int width, String start, String target)
(be sure your method is public)
    
 

Notes

-Your return value must have an absolute or relative error less than 1e-9.
 

Constraints

-distance will be between 2 and 1000, inclusive.
-width will be between 1 and 500, inclusive.
-width will be no greater than half of distance.
-start and target will be formatted as "<avenue><street>" (quotes for clarity), where <avenue> will be an uppercase letter ('A' - 'Z') and <street> will be an integer between 1 and 50, inclusive, with no leading zeros.
 

Examples

0)
    
100
10
"B1"
"B4"
Returns: 300.0

Both start and target are at the same avenue ('B'), so just go along the center of this avenue 3 blocks (each of them 100 meters long).

1)
    
100
20
"F3"
"G2"
Returns: 181.10770276274835

The example from the problem statement. An optimal path is shown by the green line in the figure in the problem statement. For the given values distance = 100 and width = 20, each of the two green segments has a length of sqrt(902 + 102) = 90.55385 meters, which gives a total of 181.1077 meters.

2)
    
1000
1
"E18"
"P9"
Returns: 19982.008508256098

For the case of such narrow streets, the optimal path is not much better than going along the center of the streets (which would be 20000.0 meters).

3)
    
8
4
"B10"
"E13"
Returns: 35.27652763864304
4)
    
120
30
"C2"
"D48"
Returns: 5584.950296406279

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=5883

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=8069&pm=5883

Writer:

gepa

Testers:

PabloGilberto , brett1479 , Olexiy

Problem categories:

Dynamic Programming, Geometry