A musician has composed several melody fragments and wants you to make a program to create a complete melody by appending those fragments. A fragment is described as a sequence of key jumps on a piano keyboard.
A piano keyboard looks like this:
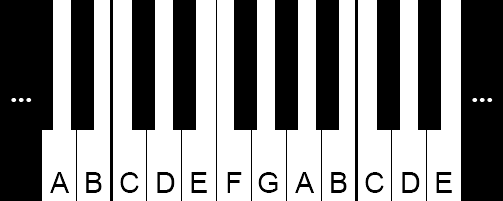
For instance, to go from the leftmost C key to the F key, a jump of 5 keys is needed (note that the black keys are counted), and to go back requires a jump of -5 keys. A fragment does not specify a starting position. It could be "2 3 -1" meaning that after the initial key we should move two keys to the right, then three and finally one to the left.
But there is a problem: the musician has set the restriction that the resulting melody must not use (including the starting position) black keys. Then, the fragment shown above could be used either starting on a G key (and then A, C and B) or starting on a C key (and then D, F and E). Each fragment can be used only once in the melody and cannot be used partially.
You are given a String[] fragments, the melody fragments, and you must return the number of fragments in the longest melody that can be created by appending those fragments. | 