Problem Statement |
| | Note: examples in this problem statement contain images which may not display properly if viewed outside the applet.
John lives in a large city and commutes to work every day. Afraid of getting hit by cars, he tends to plot his routes so that he crosses as few roads as possible, leaving home earlier if necessary. John crosses a road whenever his path intersects the road. He'll never walk along the road (on it), since that would be dangerous.
When modeled in a plane, the city is width units wide and length units long. John may never leave the city at any time. More precisely, his x-coordinate must be between 0 and width (inclusive) and his y-coordinate between 0 and length (inclusive) at all times.
You will be given the description of roads (horizontal and vertical line segments) in the city. Horizontal roads will be formatted as "y x1 x2" (quotes for clarity), vertical roads as "x y1 y2". You will also be given the coordinates of John's home and workplace, each formatted as "x y".
Return the minimum number of roads John needs to cross in order to get from home to work.
|
| |
Definition |
| | | Class: | SafeJourney | | Method: | fewestRoadCrossings | | Parameters: | int, int, String[], String[], String, String | | Returns: | int | | Method signature: | int fewestRoadCrossings(int width, int length, String[] horizontal, String[] vertical, String home, String work) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Crossing an intersection of two roads (one horizontal and one vertical) diagonally counts as crossing two roads. |
| |
Constraints |
| - | width and length will be between 1 and 2,000,000,000, inclusive. |
| - | horizontal and vertical will each contain between 0 and 50 elements, inclusive. |
| - | Each element of horizontal and vertical will be at most 50 characters long and will contain a comma-separated list of roads with at least one road. |
| - | Each road in horizontal will be formatted as "y x1 x2", where x1 is less than x2. |
| - | Each road in vertical will be formatted as "x y1 y2", where y1 is less than y2. |
| - | home and work will both be formatted as "x y". |
| - | All x-coordinates will be between 0 and width, inclusive, and all y-coordinates will be between 0 and length, inclusive. |
| - | All numbers will be integers with no leading zeros. |
| - | No two roads in horizontal will overlap and no two roads in vertical will overlap, although they may have common endpoints. |
| - | Neither home nor work will lie on a road, on either of a road's endpoints, or on the boundary of the city. |
| |
Examples |
| 0) | |
| | 6 | 4 | { "2 0 6" } | { "2 2 4", "4 0 2" } | "1 3" | "5 1" |
| Returns: 2 | | John can't get to work without crossing at least two roads.
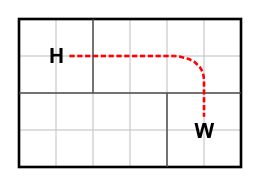
|
|
|
| 1) | |
| | 6 | 4 | { "2 0 6" } | { "2 0 2", "4 2 4" } | "1 3" | "5 1" |
| Returns: 1 | | The vertical roads have moved and John now needs to cross only one road.
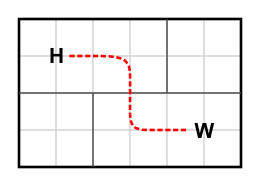
|
|
|
| 2) | |
| | 4 | 5 | { "4 1 3,1 1 3" } | { "2 1 4" } | "1 2" | "3 3" |
| Returns: 0 | |
|
| 3) | |
| | 7 | 8 | { "2 0 7", "4 0 7", "5 2 4,5 5 6", "6 0 4,6 5 7", "7 1 3" }
| { "2 2 5", "3 0 6", "4 0 7", "5 0 5" } | "1 3" | "6 1" |
| Returns: 4 | |
|
| 4) | |
| | 5 | 5 | { } | { "3 0 2", "3 2 5" } | "2 4" | "4 1" |
| Returns: 1 | | Roads will not overlap, but may have common endpoints. There is no way of getting from home to work without crossing at least one of the roads. |
|
|
| 5) | |
| | 100 | 100 | { "10 0 100,20 0 100,30 0 100,40 0 100,50 0 100",
"60 0 100,70 0 100,80 0 100,90 0 100" } | { "10 0 100,20 0 100,30 0 100,40 0 100,50 0 100",
"60 0 100,70 0 100,80 0 100,90 0 100" } | "15 6" | "93 95" |
| Returns: 17 | |
|
| 6) | |
| | 13 | 9 | { "7 0 5,6 0 5,4 4 8,4 9 13,3 4 13,2 4 8,3 1 3" } | { "1 1 3,3 0 3,4 2 7,5 2 7,7 5 9,8 5 9,8 0 1,9 1 3", "10 1 3" } | "2 8" | "2 1" |
| Returns: 1 | |
|
| 7) | |
| | 15 | 8 | { "1 9 14", "4 0 2", "6 2 3", "6 9 12", "7 0 2", "7 7 14" } | { "3 0 7", "4 1 8", "7 0 7", "9 1 6", "12 4 6", "14 1 6" } | "10 4" | "1 2" |
| Returns: 0 | |
|

