TopCoder problem "BuildBridge" used in SRM 295 (Division I Level One , Division II Level Two)

Problem Statement
	Suppose you have an infinite deck of cards all of length L and a table. What is the minimum number of cards required to build a "bridge" of length D over the edge of the table without the cards falling over? For example if you have cards of length 10 centimeters and you want to create a 7.5 centimeter bridge you must use at least 2 cards. If you used a single card it would be 7.5 centimeters over the edge and 2.5 centimeters on the table and would consequently fall down. Using one 10 centimeter card you could maximally achieve a 5 centimeter bridge since that would be the equilibrium state (5 cm on the table and 5 cm over the table). In more general terms, a stack of cards is in an equilibrium state if the center of mass of the entire stack is located above the surface of the table, and the center of mass of each contiguous substack is above the surface of the next card. 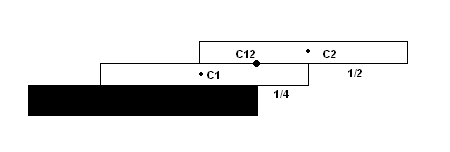Let us examine the following two cases: As you can see we have 2 cards here. The center of their mass (C12) is halfway between their centers (C1 and C2) because the cards are identical. 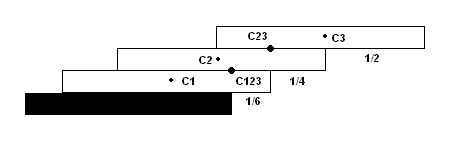Since C12 is right above the edge of the table the stack is in equlibrium and as you can't push it further forward this is the maximal extension you can get (1/4 (first card) + 1/2 (second card)) Here we have 3 cards. First observe that the top two cards are simply the case presented above with only two cards. The center of their mass is located 1/4 of the card length from the right edge of the second card. Now we use this center and the center of the first card to locate the center of the entire stack. Note however that the mass contained in C23 is twice the mass contained in C1 and therefore the resulting center of mass (C123) is located 1/6 of the card length from the right edge of the bottom card. The total extension is therefore 1/6 + 1/4 + 1/2 = 11/12 Given an int D, the distance of the "bridge" and an int L, the length of the card, what is the minimal number of cards required for a stable bridge of length D?
Definition
	Class: BuildBridge Method: howManyCards Parameters: int, int Returns: int Method signature: int howManyCards(int D, int L) (be sure your method is public)
Notes
-	Both D and L are given in centimeters.
Constraints
-	D will be between 1 and 9, inclusive.
-	L will be between 1 and 9, inclusive.
Examples
0)
	1 1 Returns: 4 3 cards extend 11/12 cm over the table edge... this is close but not enough. 4 cards extend 25/24 cm over the table edge and this is just above 1 cm. Therefore you need at least 4 one centimeter cards to build a one centimeter bridge.
1)
	1 6 Returns: 1 A single 6 cm card is more than enough for a 1 cm bridge.
2)
	3 6 Returns: 1 If you place the card exactly half-way over the edge you get a stable 3 cm bridge.
3)
	4 6 Returns: 2 You can't do more than 3 with a single card so at least 2 cards are needed.
4)
	9 1 Returns: 36865412

Problem url:

Problem stats url:

Writer:

Testers:

Problem categories: