Consider the following code, which traverses a tree and prints a sequence of characters:
bypass(Node v) {
for i=0..size(v.children)-1 {
write('1');
bypass(v.children[i]);
write('0');
}
}
Starting from the root this code will generate a string of 0's and 1's that fully describes a tree.
For example, "1101100110011000" will represent the tree in the following picture (nodes are marked in the order of traversal).
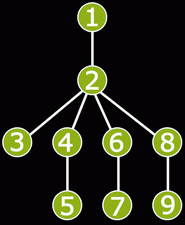
A tree is called symmetrical if, after reversing the order of children for all nodes, the string representation of the tree is not changed. For example, the tree in the picture is not symmetrical because the string representation changes to "1110011001100100" after the order of children is reversed for all nodes.
You will be given a String tree. You are to make it symmetrical by removing some nodes and changing the order of children for some nodes. You can remove a node only if all its children are removed too. You should return tree after making it symmetrical. If there are multiple ways to make tree symmetrical, you should minimize the number of removed nodes. If two or more solutions still remain, return the one that comes first lexicographically.
| 