TopCoder problem "PizzaDivision" used in SRM 312 (Division II Level Three)



Problem Statement

    

You want to divide a round pizza (represented by a circle) into two equal halves with one straight cut. The pizza contains several toppings, represented by points strictly inside the circle. The cut is called beautiful if the two halves of the pizza are mirror images of each other: for every topping in one half there is a topping in the other half in the symmetric point (we don't care about the toppings that are exactly on the cut).

For example, the cut represented by the red line in the following picture is the only beautiful cut for that pizza (black dots are toppings):

This pizza has four different beautiful cuts, all shown by red lines:

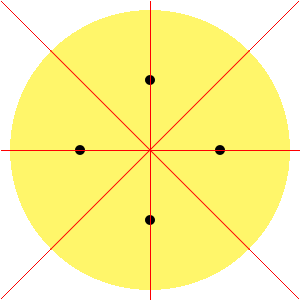
You are to count the number of different beautiful cuts for a given pizza. You are given a String[] toppings, each element representing a topping in the form "x y", where x and y are the coordinates of that topping. You may assume that the pizza is large enough to have all those toppings inside. The point of origin coincides with the center of the pizza (that is, the center of the pizza has the coordinates "0 0"). Return the number of different beautiful cuts, or -1 if there are infinitely many of them.

 

Definition

    
Class:PizzaDivision
Method:howMany
Parameters:String[]
Returns:int
Method signature:int howMany(String[] toppings)
(be sure your method is public)
    
 

Notes

-Two points A and B are symmetric with respect to line L, if and only if either A and B coincide and lie on L or L is perpendicular to AB and crosses it in its middle point.
 

Constraints

-toppings will contain between 1 and 50 elements, inclusive.
-Each element of toppings will be formatted as "x y" (quotes for clarity only), where x and y are integers between -500 and 500, inclusive, with no extra leading zeroes.
-All elements of toppings will be different.
 

Examples

0)
    
{"0 110", "0 70", "-75 20", "75 20", "-25 -50", "25 -50"}
Returns: 1
The first example from the problem statement.
1)
    
{"0 70", "70 0", "0 -70", "-70 0"}
Returns: 4
The second example from the problem statement.
2)
    
{"0 0"}
Returns: -1
Any cut passing through the center suffices.
3)
    
{"3 -4"}
Returns: 1
4)
    
{"3 -4", "-3 4"}
Returns: 2
5)
    
{"1 2", "3 4"}
Returns: 0
6)
    
{"-300 100", "-200 100", "-100 100", "100 100", 
"200 100", "300 100", "-300 -100", "-200 -100", 
"-100 -100", "100 -100", "200 -100", "300 -100"}
Returns: 2
7)
    
{"-54 -83", "-46 54", "-5 -44", "-1 -31", "-14 47", 
"7 -5", "-45 -63", "-88 47", "-17 -9", "-26 -66", 
"40 56", "-67 69", "-49 -2", "2 62", "61 78", 
"-81 -32", "87 33", "-22 -53", "-43 -38", "57 28", 
"35 12", "-53 -15", "52 -16", "32 -44", "-73 68", 
"79 44", "3 56", "-66 26", "-87 41", "4 87", 
"22 53", "59 16", "-3 55", "3 19", "-26 8", 
"43 38", "54 46", "-16 22", "-3 -93", "45 63", 
"0 -37", "-7 5", "-40 -56", "40 19", "-8 -63", 
"-16 -89", "29 11", "-52 -21", "-58 -22", "4 -61"}
Returns: 1

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6493

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9992&pm=6493

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Yarin , Olexiy

Problem categories:

Geometry, Simple Math, Simple Search, Iteration