Problem Statement
The game Battleship is a guessing game played by two people. The game is played on a board of square grids, normally 10x10. Each ship occupies a number of consecutive squares on the board, arranged either horizontally or vertically, but not overlapping each other. The lengths of the ships are given before the game, for example:
- one ship of length 5
- two ships of length 4
- one ship of length 3
In the game, the two players take turns choosing a single square from the opponent's board, and shooting at it. The player whose ships are being shot at then announces whether any ship was hit. If all the grids that a single ship occupies have been hit, that ship is sunk. If all of a player's ships are sunk, that player loses.
In this problem we consider a more advanced version of the game. During each turn you may shoot at multiple squares at the same time. As feedback, you will be given the number of shots that hit each ship, but not told which shots they were. Your goal is to sink all the ships as soon as possible. (You are only playing as an attacker -- you don't have to place ships).
You should write a method play that takes a int size, a int[] ships, and a int fireNum. size gives the length and width of the board. ships gives the sizes of the ships (one per element). fireNum gives the maximum number of shots that you may fire in one turn. For each set of shots, your method should call a static function fire in class Battleship which takes int[]s x and y giving the coordinates of your shots (x and y coordinates are indexed from 1). This function will return a int[] telling you how many of your shots hit each ship (elements of this return correspond to elements of ships). Once you have sunk every ship, you should return your favorite integer from your play method (this value will be ignored). Failure to sink every ship will result in a score of 0.
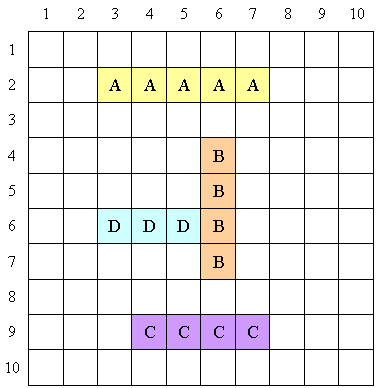
Consider this example where size=10 and ships={5,4,4,3}.
During the first turn, you fire six shots: (4,2), (5,3), (6,4), (7,5), (6,6), and (5,6) (do this by calling fire({4,5,6,7,6,5},{2,3,4,5,6,6})).
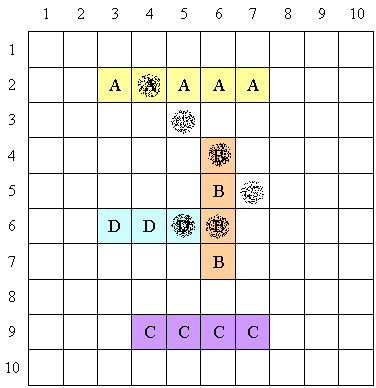
The fire method would then return {1,2,0,1} meaning that you successfully hit 1, 2, 0, and 1 grids respectively for ship A, B, C and D.
You would then continue to fire more shots by making more calls to fire.
The scoring is based on the time it takes you to sink each ship. Suppose you sink the ship with index i at turn t[i] (your first set of shots are at turn 1), you will get a penalty of shipLength[i] * t[i]. Your total penalty for a test case will be the sum of the penalties for all the ships (this is what is reported as your score when you test the examples). Your final score for each test case will be based on how far your total penalty is from the lowest total penalty out of all competitors. For a particular test case, the best penalty will be found (call this best and your penalty pen). Your score will be the sum over all test cases of best/pen. So, if your penalty for a particular test case was 600, and the best penalty for that test case was 590, your score for that case would be 590/600.
The test cases are generated as follows: size will be chosen uniformly between 6 and 50, inclusive. fireNum will be chosen uniformly between 2 and size, inclusive. The number of ships will be equal to floor(size/2). Ships will be placed one at a time. First, an initial length for a ship is uniformly chosen between 2 and floor(size / 3 + 2), inclusive. Then the legal positionings (no conflict with the ships already placed) for that ship will be calculated. Whenever no legal positioning is found, the size will be decreased by one and the positionings will be recalculated. Afterwards, a random positioning will be chosen among all the legal ones.
Definition
| Class: | BattleshipGame |
| Method: | play |
| Parameters: | int, int[], int |
| Returns: | int |
| Method signature: | int play(int size, int[] ships, int fireNum) |
| (be sure your method is public) | |
Notes
Examples
| ||
Returns: "fireNum = 3 .....B.. .....B.. .......C AADD...C .......C ........ ........ ........ " | ||
| ||
Returns: "fireNum = 8 ..A..... ..A..... ....C..D ....C..D ....C..D ........ ........ ..BBB... " | ||
| ||
Returns: "fireNum = 3 ....................P....................G... ....................P....................G... ....................P....................G... ....................P....................G... LLLLLLLLLLL.........P....................G... ..........RR........P....................G... ....................P.F..................G... ....................P.F..................G... ....................P.F..................G... ....................P.F..................G... ....................P.F..................G... ....................P.F..................G... ....................P.F..........VVVVVVVVG... ....................P.F..................G... ....................P.F..................G... EH.............BBBBBBBBBBBBBB............G... EH.....................................AAA... EH............MMMMMMMMMMMMMMMM............... E............................................ E.......................U.................... E....DDDDDDDDDDDDDDDD...U.................... E.TTTTTTTTTTT...........U..................OO E.......................U.................... E.......................U.................... E.......................U.................... E...C...................U.................... E...C...................U.................... E...C...................U.................... E...C...................U.J.................. E...C...................U.J..N............... E.Q.C........S..........U.J..N............... ..Q.C........S..........U.J..N............... ..Q.C........S............J..N............... ..Q.C........S............J..N............... ..Q.C........S............J..N............... ..Q.C........S............J..N............... ..Q.C........S............J..N..............I ..Q.C.....................J.................I ....C.....................J.................I ..........................J.................I ............................................I ............................................I ............................................I ...........................KKKK.............I ............................................I " | ||
| ||
Returns: "fireNum = 14 ............... .......DDDDDD.. .............E. .............EG .............EG B............EG B............EG B.............G B.............. B.............. ..AAAAAAF...... ........F...... ............... ....CCCC....... ............... " | ||
| ||
Returns: "fireNum = 26 .................................... .................................... .........................PPPPPPPPP.. .................................... .................................... .................................... ............K.MMMMMMMMMMMM.......... ............K...EEEEEEEE............ ............K....Q............D..... ............K....Q............D..... ....RRRRRRRRK....Q.................. ............K....Q.............BBBBB .HHHHHHHHH..K....QI................. .........O..K....QI......C.......... .........O..K....Q.......C.......... .........O..K....Q.......C.......... ........GO.......Q.......C.......... ........GO.......Q.......C...F...... ........GO.......Q.......C...F...L.. ........GO.......Q.......C...F...L.. ........GO.......Q.......C...F...L.. ........GO...............C...F...L.. ........GONNNNNNNNNN.....C.......L.. ........GO...............C.......L.. ........GO....JJJJJJJJJ..........L.. ........GO.......................L.. ........G........................L.. ........G........................L.. ......AAAAAAAAA..................L.. .................................L.. .................................L.. .................................... .................................... .................................... .................................... .................................... " | ||
| ||
Returns: "fireNum = 45 ................................................ ................................................ ................................................ .............................................I.. ..................................L..........I.. ..................................L..CCCCCCCCI.. ......HHHHHHHHHHHHHHHH............L..........I.. ....................OOOOOOOOOOOO..L..........I.. ..................................L..........I.. ..................................L..........I.. ...............................RR.L..........I.. ..................................L..........I.. ..................................L............. ..................................L............. .......EEEEEEEEEEEEE............................ ................................................ ..........................................W..... .......U..................................W..... .......U..................................W..... .......U........................................ ..B....U....M...............NNNNNNNNNNNNNNNNN... ..B....U....M................................... ..B....U....M.............................S..... .......U....MDDDDDDDDDDDDDDD..............S..... .......U....M.............................S..... .......U....M...........GGG...............S..... .......U....M.............................S..... .......U....M.............................S..... ...T...U....M.............................S..... ...T...U..................................S..... ...T...U..................................S..... ...T...U..................................S..... ...T...U.....K............................S..... ...T...U.....K............................S..... ...T.........K.................................. ...TJJJJ.....K.................................. ...T.........K...........XXXXX......QQQQQQ...... ...T.........K.........................A........ ...T.........K.........FFF.............A........ .............K.............PPPPPPPPP...A........ .............K.........................A........ .............K......V..................A........ .............K......V..................A........ .............K.........................A........ .............K.................................. .............K.................................. .............K.................................. ................................................ " | ||
| ||
Returns: "fireNum = 3 .......... .......... ..E....... ..E....... ...DD..... .....C.AA. .....CBB.. .....C.... .......... .......... " | ||
| ||
Returns: "fireNum = 2 .....AAA.... ............ D........... D........... D........... D........... ............ ............ .........CE. ..B......CE. ..B.......E. ........FFFF " | ||
| ||
Returns: "fireNum = 9 ............................................. ............................................. ............................................. ............................................. ............................................. ............................AAAAAAAAAAAAAAAA. ............................................. ............................................. ............................................. ............................................. .QQQQQQQQQQQQ................................ ................OOOOOOOOOOOOOOO.............. ............................................. ............................................. ............................................. ..........................B.................. ..........................B.................. .........................S................... .........................S................... .........................S................... ................U........S..HHHHHHHHHHHHHHHH. ................U........S..................N ................U........S..................N ................U.J.........................N ...............TU.J.........................N ...............TU.JLLLLLLLLL................N ...............TU.J.........................N .........CCCCCCTU.J.........................N ...............TU.J...E.....................N I..............T..J...E.....................N I..............T......E................F....N I..............T......E....R...........F....N I..............T......E....R...........F..M.N I..............T......E....RP..........F..M.N I..............T......E....RP..........FG.M.N I..............T..D...E....RP..........FG.M.. I..............T..D...E....RP..........F..M.. I..........KKKKK..D...E....RP...V......F..M.. I.................D........RP...V......F..... ..................D........RP...V......F..... ...........................RP...V......F..... ...........................RP..........F..... ...........................R................. ............................................. ............................................. " | ||
| ||
Returns: "fireNum = 27 ..................................... ...LKKKKKKKKKKKK..................... ...L................................. ...L....OOOOOOOOOO................... ...L................................. ..EL.IIIIIIIIIII..................... ..EL................................. ..EL...................QQQ........... ..EL...............................HH ..EL................F................ ..E.................F................ ..E.................F................ ..E.................F...............A ..E.....BBBBBBBBBBBBF...............A ..E.................F...............A ..E.................................A ....................................A ....................................A ....................................A ....................................A ...........PPPP...J.................A ..................J.................A ..................J.................A ..............MMM.J.................A ..................J.................A ..................J.................. ..................J.....NN........... ..CCCC............J.................. ..................J............GGGGGG ..................J.................. ..................J.................. ..................J.................. ...............DDDDDDDDDDDD.......... ..................................... .......RRRRRRRRRRRR.................. ..................................... ..................................... " | ||