Consider a N-level pyramid built of unit cubes. An example for N=3 can be seen in the image below.
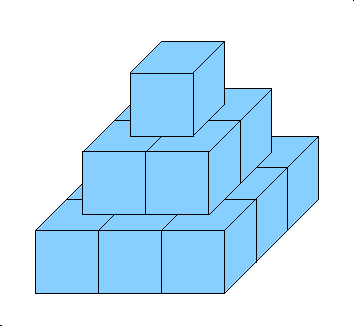
Formally, a pyramid of size N has N levels, where the i-th level (counting from the top) contains an i by i grid of unit cubes.
You have K cubes. First, you select a suitable pyramid size as follows: If K is exactly the number of cubes necessary to build a pyramid of size N for some N, you pick that size. Otherwise, you pick the smallest pyramid size you can not build.
Now you start building the pyramid in a systematic bottom-up way. First you build the complete bottom level, then you build the level above that, etc. When building a level, also proceed in a systematic way, starting the next row only when the previous one is full.
For example, for 21 cubes you should get the following incomplete pyramid:
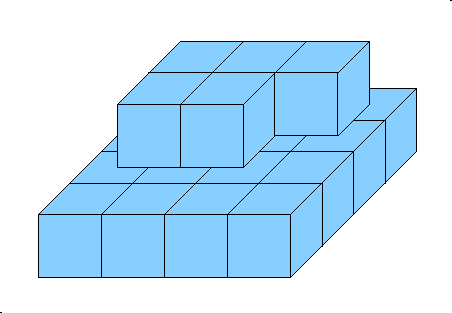
Given an int K specifying the number of cubes you have, return the surface area of the possibly incomplete pyramid you will build according to the instructions above.
| 
