TopCoder problem "TopologicalEquivalence" used in TCCC06 Round 3 (Division I Level Three)



Problem Statement

    

Consider the figures made up of line segments below. There are 5 connected figures, but only 3 distinct figures if one considers their topological features (the first and second are equivalent, as are the third and fourth). Two figures are considered to be topological equivalent if one of the figures can be deformed by stretching, bending, etc. into the other (but not necessarily in 2D space).

A more formal definition can be expressed in terms of graph theory. A figure can be considered to be an embedding of a multigraph (it may have loops and multiple edges) in the plane, where each vertex has been assigned to a distinct point, and each edge to some polygonal path without self-intersections. We consider two figures to be equivalent if their embeddings could have both originated from the same multigraph. In this problem, we will assume that each edge is disjointly embedded. That is, two embedded edges can only meet at a common endpoint.



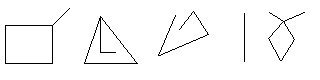
Create a class TopologicalEquivalence containing the method countDistinct which takes a set of non-intersecting and non-overlapping line segments and counts the number of distinct connected figures (according to the definition of topological equivalence above). The line segments will be given in a String[] lineSegs, where each element may contain several line segments. A line segment will be given in the form (quotes for clarity) "x1,y1-x2,y2" and within each element they will be single space separated. Two line segments are connected if they share a common endpoint. A figure is a minimal non-empty subset of the line segments such that no line segment in the figure is connected to a line segment not in the figure.

 

Definition

    
Class:TopologicalEquivalence
Method:countDistinct
Parameters:String[]
Returns:int
Method signature:int countDistinct(String[] lineSegs)
(be sure your method is public)
    
 

Constraints

-The line segments making up a figure will have at most 8 distinct end points.
-lineSegs will contain between 1 and 50 elements, inclusive.
-Each element in lineSegs will contain between 7 and 50 characters, inclusive.
-Each element in lineSegs will be a space-separated list of line segments specified in the format above. There will be no leading, trailing, or consecutive spaces.
-The coordinates for each line segment will be integers between 0 and 1000, inclusive, with no extra leading zeros.
-No two line segments will partially overlap or intersect, except at the endpoints.
-All line segments will have a positive length.
 

Examples

0)
    
{"0,7-5,7 5,7-5,2 5,2-0,2 0,2-0,7 5,2-7,0",
 "8,7-15,7 15,7-10,2 10,2-8,7 10,2-10,5 10,5-12,5",
 "16,6-19,2 16,6-22,4 22,4-21,2 21,2-19,4",
 "24,7-24,2",
 "25,5-27,3 27,7-29,5 25,2-27,3 29,2-27,3 25,5-27,7","27,3-29,5"}

Returns: 3
This corresponds to the figures in the pictures. Here, each element correspond to one of the figures (although this is not generally the case, see further examples).
1)
    
{"16,0-17,1 17,1-17,3 17,3-16,4 16,4-14,4 14,4-14,0",
 "9,1-9,3 9,3-10,4 10,4-12,4 12,4-13,3 14,0-16,0",
 "0,4-1,2 1,2-2,0 2,0-3,2 1,2-3,2 3,2-4,4 5,0-7,0",
 "25,0-27,0 24,1-24,3 24,3-25,4 25,4-27,4 27,4-27,2",
 "7,0-8,1 8,1-7,2 7,2-8,3 8,3-7,4 7,4-5,4 5,4-5,2",
 "18,0-20,0 18,0-18,2 18,2-18,3 18,2-18,4 18,4-20,4",
 "21,0-23,0 21,0-21,2 21,2-22,2 21,2-21,4 24,1-25,0",
 "5,2-5,0 5,2-7,2 9,1-10,0 10,0-12,0 12,0-13,1",
 "27,2-25,2 28,0-28,2 28,2-28,4 30,0-30,2 30,2-30,4",
 "28,2-30,2 31,0-31,4"}

Returns: 6
The 9 figures in this input correspond to the letters A, B, C, D, E, F, G, H and I. Topologically, the three letters C, G and I are the same, as well as the two letters E and F. The remaining 4 letters have distinct topological features.
2)
    
{"0,2-2,2 10,2-12,0 2,2-4,0 12,0-14,2",
 "4,0-4,4 14,2-10,2 4,4-2,2 10,2-12,4",
 "4,4-6,2 12,4-14,2 6,2-8,2 12,4-12,6",
 "14,8-12,6 6,2-4,0 12,6-10,8"}


Returns: 2

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6648

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10111&pm=6648

Writer:

Yarin

Testers:

PabloGilberto , brett1479 , radeye , Olexiy

Problem categories:

Brute Force, Graph Theory