TopCoder problem "IncompleteBST" used in SRM 319 (Division II Level Three)



Problem Statement

    This statement contains images which must be viewed in the applet.

A Binary Search Tree (BST) is a tree data structure which obeys the following properties:

  • Each node has at most 2 children.
  • Each node except the root has exactly 1 parent.
  • There is exactly 1 root node. The root node does not have any parents.
  • If a node has a left child, all values in the left subtree are less than or equal to the value of the node itself.
  • If a node has a right child, all values in the right subtree are strictly greater than the value of the node itself.

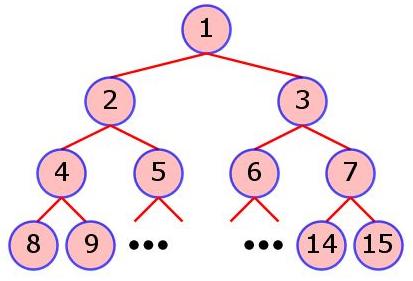
In this problem, nodes are identified starting from the root node as 1, and following in order with nodes at the next level, etc. See the figure below for clarification.

You will be given a BST with one node value that is missing. You must determine the possible values that the node can represent so as to maintain a valid BST according to the above rules.

Create a class IncompleteBST that contains a method missingValues. The method takes a String[] tree as input and returns a String corresponding to the possible values (from among 'A' to 'Z') that the missing character can assume so as to maintain a valid BST. Each element of tree is formatted as follows: "CHARACTER INTEGER" (quotes for clarity only). That is, a single character followed by a single space followed by a single integer. The CHARACTER denotes the value of the particular node in the BST. In exactly one element of tree, CHARACTER will be '?', denoting the unknown missing value. The INTEGER denotes a particular node in the BST according to the above numbering scheme.

Note that tree will always contain a root node numbered 1. Furthermore, tree will represent a connected tree, that is, all nodes present in the tree will be reachable from the root node. The returned String must be sorted in ascending order and must contain distinct values only. If tree does not represent a valid BST, return an empty string; see the examples for clarification.

 

Definition

    
Class:IncompleteBST
Method:missingValues
Parameters:String[]
Returns:String
Method signature:String missingValues(String[] tree)
(be sure your method is public)
    
 

Constraints

-tree will contain between 1 and 20 elements, inclusive.
-tree will represent a connected tree.
-Each element of tree will be formatted as described, "CHARACTER INTEGER".
-Each INTEGER will be an integer between 1 and 220-1, inclusive, with no leading zeroes.
-Exactly one INTEGER will be equal to 1. That is, there will be a root node in tree.
-Each INTEGER in tree will be distinct.
-Each CHARACTER will be an uppercase letter ('A'-'Z') or '?'.
-Exactly one CHARACTER will be '?'.
 

Examples

0)
    
{"A 1", "? 2"}
Returns: "A"
In this case, the tree consists of a root node and a single left child. Thus, the missing value can be any letter whose value is less than or equal to 'A', namely "A".
1)
    
{"B 1", "? 2"}
Returns: "AB"
This case is similar to the previous one, except the root value is now a 'B'. Thus, the left child can be any value less than or equal to 'B', namely "AB".
2)
    
{"V 1", "? 3"}
Returns: "WXYZ"
3)
    
{"K 1", "K 2", "A 6", "? 12", "Y 3"}
Returns: ""
The tree described by the input may not be a valid BST! In this case, the node with value 'A' cannot be in the subtree formed by the right child of the root node, since 'A' is a smaller value than 'K'.
4)
    
{"Z 1", "Y 2", "X 4", "W 8", "V 16", "U 32", "T 64", "S 128", "R 256", "Q 512", 
"P 1024", "O 2048", "N 4096", "M 8192", "L 16384", "K 32768", "J 65536", "? 131072"}
Returns: "ABCDEFGHIJ"

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=6713

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=9999&pm=6713

Writer:

NeverMore

Testers:

PabloGilberto , brett1479 , Olexiy , ged

Problem categories:

Brute Force, Recursion