| This statement contains images which must be viewed in the applet.
A Binary Search Tree (BST) is a tree data structure which obeys the following properties:
- Each node has at most 2 children.
- Each node except the root has exactly 1 parent.
- There is exactly 1 root node. The root node does not have any parents.
- If a node has a left child, all values in the left subtree are less than or equal to the value of the node itself.
- If a node has a right child, all values in the right subtree are strictly greater than the value of the node itself.
A BST is constructed from a string of characters in the following way: The root node of the tree is assigned the value of the first character in the string. All subsequent characters are added as children of existing nodes subject to the above rules. Note that the tree is never altered in any other manner. In this problem, nodes are identified starting from the root node as 1, and following in order with nodes at the next level, etc. See the figure below for clarification.
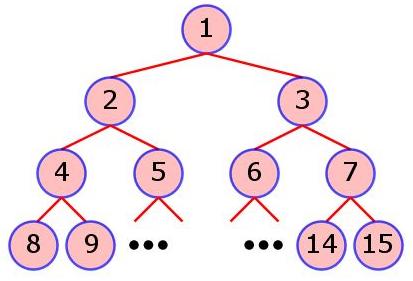
You will be given the shape of a particular BST by specifying the identities of the nodes which constitute the tree, according to the above scheme. Note that you do not know the exact input string used to construct the given BST. You do know, however, that the first N uppercase letters were used to construct the given BST with N nodes. See the examples below for further clarification.
Create a class ConstructBST that contains a method numInputs. The method takes an int[] tree with a list of node numbers present in the tree and returns a long corresponding to the number of strings composed of the characters from 'A' to 'Z' that could have been used to produce the particular BST. Note that tree will always contain a root node numbered 1. Note also, that tree will represent a connected tree, that is, all nodes present in the tree will be reachable from the root node.
|