TopCoder problem "HiddenSquares" used in SRM 331 (Division I Level Three)



Problem Statement

    

Little Greg got a set of pencils for Christmas. Since then, he has been spending hours drawing rectangles on a piece of paper. In this problem, the paper will be represented as an x-y plane. All the rectangles have sides parallel to the axes, and some of them may intersect, creating even more rectangles. Greg wonders how many squares (rectangles with sides of equal length) exist in his drawing.

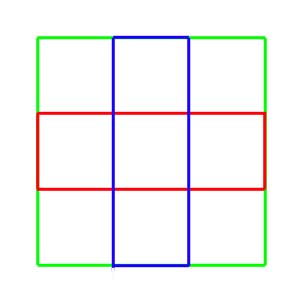
For example, in the image below, Greg has drawn three rectangles, one in red, one in green, and one in blue. These three rectangles intersect to form a total of 36 rectangles, 14 of which are squares (nine 1 x 1, four 2 x 2, and one 3 x 3).

You are given the rectangles drawn by Greg in the int[]s x1, y1, x2, and y2. (x1[i], y1[i]) is the lower left corner of the ith rectangle, and (x2[i], y2[i]) is the upper right corner of the ith rectangle. Return the number of squares that exist in the drawing.

 

Definition

    
Class:HiddenSquares
Method:count
Parameters:int[], int[], int[], int[]
Returns:int
Method signature:int count(int[] x1, int[] y1, int[] x2, int[] y2)
(be sure your method is public)
    
 

Constraints

-x1, y1, x2, and y2 will each contain between 1 and 50 elements, inclusive.
-x1, y1, x2, and y2 will each contain the same number of elements.
-Each element of x1, y1, x2, and y2 will be between 0 and 1000000000, inclusive.
-For all i, x1[i] will be less than x2[i], and y1[i] will be less than y2[i].
 

Examples

0)
    
{0,1,0}
{0,0,1}
{3,2,3}
{3,3,2}
Returns: 14
The example from the problem statement.
1)
    
{0,2}
{0,0}
{2,4}
{4,4}
Returns: 1
These two rectangles combine to form a single square.
2)
    
{0,0,3}
{0,3,0}
{1,4,4}
{3,4,3}
Returns: 0
There are no squares here.
3)
    
{453453463,453453500,453453495,453453512,453453478,453453489,
 453453466,453453500,453453498,453453510,453453472,453453512,
 453453519,453453514,453453521,453453518,453453523,453453517,
 453453466,453453525,453453496,453453495,453453463,453453461,
 453453460,453453522,453453471,453453468,453453479,453453517,
 453453485,453453518,453453499,453453464,453453494}
{364646438,364646402,364646449,364646438,364646415,364646401,
 364646446,364646416,364646456,364646414,364646463,364646407,
 364646436,364646450,364646421,364646411,364646414,364646419,
 364646445,364646427,364646405,364646442,364646418,364646464,
 364646457,364646463,364646432,364646426,364646444,364646431,
 364646450,364646418,364646434,364646458,364646402}
{453453488,453453510,453453525,453453523,453453493,453453500,
 453453470,453453511,453453499,453453521,453453518,453453524,
 453453523,453453523,453453524,453453523,453453525,453453519,
 453453473,453453526,453453511,453453517,453453470,453453464,
 453453511,453453524,453453516,453453516,453453492,453453524,
453453513,453453522,453453520,453453505,453453512}
{364646460,364646454,364646462,364646466,364646464,364646455,
 364646457,364646461,364646457,364646450,364646466,364646453,
 364646441,364646451,364646460,364646461,364646446,364646464,
 364646447,364646460,364646454,364646450,364646444,364646466,
 364646458,364646466,364646455,364646442,364646462,364646435,
 364646464,364646444,364646455,364646459,364646430}
Returns: 124

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7265

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10011&pm=7265

Writer:

slex

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem categories:

Geometry