TopCoder problem "BeautifulHexagonalTilings" used in SRM 355 (Division I Level Three)



Problem Statement

    

Consider a hexagonal grid with 6 sides, with the side lengths given by the int[] s (in the clockwise order), as shown in the following picture:

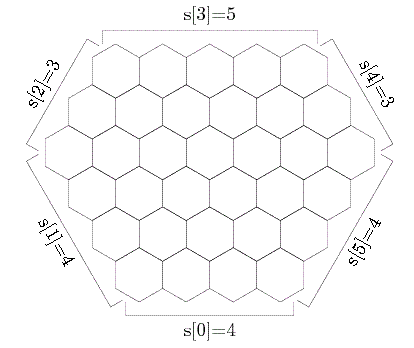
Count the number of ways to color each cell with one of two colors, black or white, such that every non-border black cell has exactly a black neighbors, and every non-border white cell has exactly b white neighbors (a cell is called non-border if and only if it has exactly 6 neighbors in the grid).

 

Definition

    
Class:BeautifulHexagonalTilings
Method:howMany
Parameters:int[], int, int
Returns:int
Method signature:int howMany(int[] s, int a, int b)
(be sure your method is public)
    
 

Constraints

-s will contain exactly 6 elements.
-Each element of s will be between 2 and 6, inclusive.
-a and b will each be between 0 and 6, inclusive.
-s will define a valid hexagonal grid.
-The answer will always fit into an int.
 

Examples

0)
    
{2,2,2,2,2,2}
6
6
Returns: 2
Either all white or all black.
1)
    
{6,6,6,6,6,6}
6
6
Returns: 2
The field is bigger, but still all white or all black.
2)
    
{2,2,2,2,2,2}
2
2
Returns: 30
3)
    
{4,4,3,5,3,4}
4
1
Returns: 213
The grid from the picture.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7761

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10712&pm=7761

Writer:

Petr

Testers:

PabloGilberto , brett1479 , Olexiy , marian

Problem categories:

Brute Force, Search