Quicksort is one of the most well-known sorting algorithms. On average it makes O(N log(N))
element comparisons, although in the worst case the number of comparisons is O(n2). The critical
part in Quicksort is the selection of the pivot element. If one knows the details of a specific Quicksort
implementation, it is generally possible to exploit this and create an input sequence which will cause
that implementation to perform badly. This can for instance be used by malicious users to cause time-outs in
critical system components that rely too much on the efficiency of Quicksort.
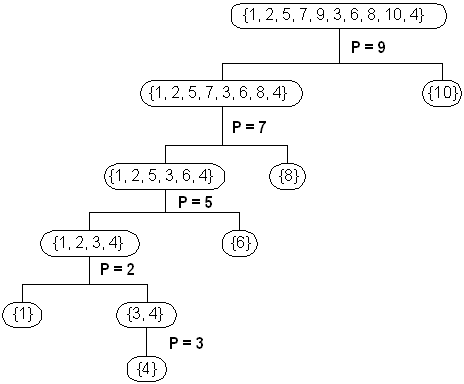
Given the details of a specific Quicksort algorithm (pseudocode below), your task is to generate a sequence
of n distinct integers between 1 and n, inclusive, that causes this Quicksort to reach the largest nesting
depth (see examples for further clarifications).
function quicksort(list q)
var list less, greater
if length(q) <= 1
return q
select a pivot value pivot from q
for each x in q
if x < pivot then add x to less
if x > pivot then add x to greater
return concatenate(quicksort(less), [pivot], quicksort(greater))
The pivot element selected in the pseudocode will be the median of three elements in q. The relative position of these three elements
will be given by the input parameter positions, containing three integers between 0 and 999, inclusive. If the number
of elements in q is k, the position (0-indexed) for the three elements that will be considered as pivot
elements will thus be (k * positions[x]) / 1000 (rounded down) for each x between 0 and 2, inclusive. The most common pivot
selection method is to take the median of the first, the middle and the last element, which would correspond to positions = {0, 500, 999}.
Create a class WorstCaseQuicksort containing the method worstInput which takes as input an int n
and a int[] positions and returns a int[] with n distinct integers between 1 and n,
inclusive, so that the largest nesting depth is reached. Since there are many such int[]s, return the
one that comes first lexicographically (see notes).
|