Problem Statement |
| | An array of integers is called convex if all of the following apply:
- It contains an even number of elements.
- It contains between 6 and 50 elements, inclusive.
- Each element is an integer between 1 and 50, inclusive. Interpret the integers as the coordinates of n points: x_1, y_1, x_2, y_2, ..., x_n, y_n (in this order).
- These n points are vertices of a convex polygon.
- The vertices are listed in either clockwise or counterclockwise order.
- No three consecutive vertices lie on the same straight line (when saying three consecutive vertices we also mean vertices number N, 1 and 2 and vertices number N-1, N and 1).
Given a int[] beginning, find the shortest int[] that will produce a valid convex array when appended to the end of beginning. If there are multiple such int[]s, return the one among them that comes first lexicographically. If there is no such int[], return a int[] containing a single element -1.
|
| |
Definition |
| | | Class: | ConvexArray | | Method: | getEnding | | Parameters: | int[] | | Returns: | int[] | | Method signature: | int[] getEnding(int[] beginning) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | beginning will contain between 0 and 50 elements, inclusive. |
| - | Each element of beginning will be between 1 and 50, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: {1, 2 } | | The polygon must contain at least 3 points, so we need to add at least one more. Adding (1, 1) would give us a segment, not a polygon, thus we stick to the next lexicographical point which is (1, 2). |
|
|
| 1) | |
| | | Returns: {1, 1, 1 } | | It is possible that the x coordinate is given and you have to choose the y coordinate. |
|
|
| 2) | |
| | | Returns: {1, 1, 2, 1 } | | (1, 1, 1, X) would form a segment, not a triangle. Move on to the next lexicographical quadruple, (1, 1, 2, 1). |
|
|
| 3) | |
| | | Returns: {4 } | 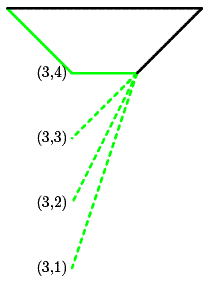
We need to find the y coordinate for the last vertex that will generate a convex polygon. Points (3, 1) and (3, 2) would make the polygon non-convex. Point (3, 3) would break the rules because there would be three consecutive vertices on the same straight line. Point (3, 4) is the only valid choice. |
|
|
| 4) | |
| | {1, 1, 2, 3, 3, 1, 1, 2, 3} |
| Returns: {-1 } | 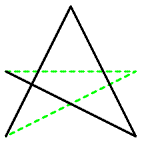
No matter what the last y-coordinate is, the edge (1, 1)-(2, 3) intersects the edge (3, 1)-(1, 2), so there is no convex polygon possible. |
|
|

