TopCoder problem "TrianglesBoard" used in TCHS SRM 41 (Division I Level Three)



Problem Statement

    

You are given a triangular board of cells, where each cell is an equilateral triangle. Cells are arranged as shown in the picture below.

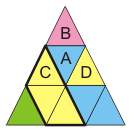
Two cells are adjacent if they have a common edge. Thus, in the example above, cells B, C and D are adjacent to cell A. There are three types of cells: "colored", "remove adjacent" and "remove row". A colored cell has a color between 0 and 9, inclusive. The other two types of cells have no color. You will choose one cell and remove it. You will then possibly remove more cells recursively according to the following rules:

  • If you removed a colored cell, you must recursively remove all adjacent colored cells with the same color.
  • If you removed a "remove adjacent" cell, you must recursively remove all adjacent cells, regardless of their types.
  • If you removed a "remove row" cell, you must recursively remove all the cells in that same row, regardless of their types.
"Recursively removing a cell" means that you must remove this cell, check its type and apply the corresponding rule to it to recursively remove more cells (see examples 3-6 for further clarification). You can remove a cell only once, i.e., you can not remove a cell if it was removed before.

You are given a String[] board containing the rows of the board from top to bottom. Each element of board represents a single row of cells. Element i (0-based) of board contains exactly 2*i+1 characters, each representing a single cell. 'A' represents "remove adjacent" cells, 'R' represents "remove row" cells, and the digits '0'-'9' represent colored cells with colors 0 through 9, respectively.

Your total score is the number of colored cells you removed (so "remove adjacent" and "remove row" cells do not count toward your score). Return the maximal score you can get on the given board.

 

Definition

    
Class:TrianglesBoard
Method:maxScore
Parameters:String[]
Returns:int
Method signature:int maxScore(String[] board)
(be sure your method is public)
    
 

Constraints

-board will contain between 1 and 50 elements, inclusive.
-Element i of board will contain exactly 2*i+1 characters.
-Each character in board will be 'A', 'R' or '0'-'9'.
 

Examples

0)
    
{ "0",
 "121",
"31122"}
Returns: 3
The example from the problem statement. The biggest block of cells of the same color is three '1's.
1)
    
{ "1",
 "121",
"12121"}
Returns: 1
There are no two adjacent cells of the same color, so we can remove at most one cell.
2)
    
{"1",
"1A1"}
Returns: 3
We can remove all cells if we start with the "remove adjacent" cell.
3)
    
{  "2",
  "122",
 "1A122",
"2222222"}
Returns: 12
If we start removing from the topmost '2', we'll have to remove the '2' below it. After that we have to apply first rule again and remove the '2' to the right of the previous one, and so on. In such way we can remove all '2' cells on the board.
4)
    
{  "2",
  "224",
 "12R43",
"R111333"}
Returns: 14
Removing the 'R' in the middle of the board will result in removing '1','2','3' and '4' in the same row, and removing each of the colored cells will result in removing all cells of the same color on the board.
5)
    
{   "R",
   "2AR",
  "R12A2",
 "2A2121R",
"R121212A2"}
Returns: 16
We need to start with the 'R' cell in lower-left corner. Removing it will remove all cells in the lowest row. Removing the 'A' cell in the lowest row will remove the 'R' cell above it, which will result in removing the second lowest row, etc.
6)
    
{ "A",
 "AAA",
"AAAAA"}
Returns: 0
Removing 'A' cells is recursive too, so we can remove all cells on the board, but there are no colored cells on it, so the score will be 0.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=7902

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10788&pm=7902

Writer:

Nickolas

Testers:

PabloGilberto , brett1479 , Olexiy , ivan_metelsky

Problem categories:

Search, String Manipulation