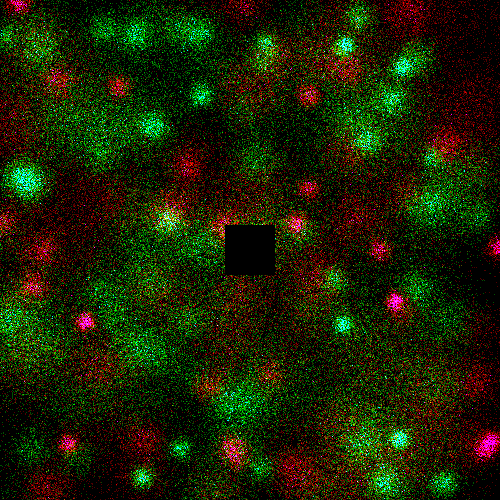
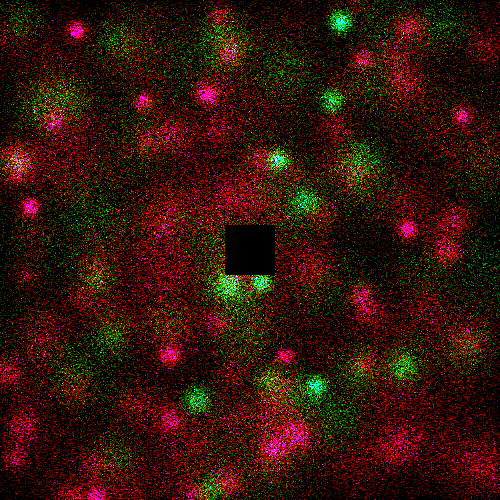
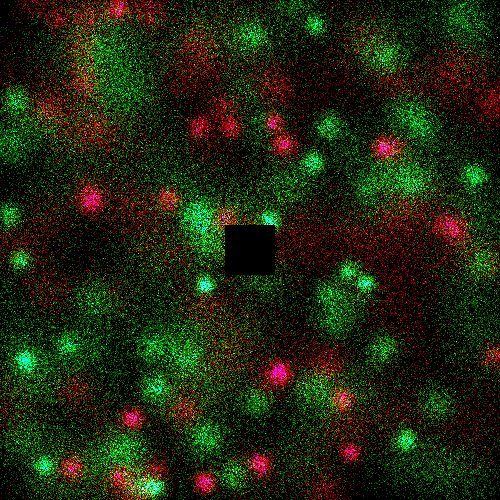
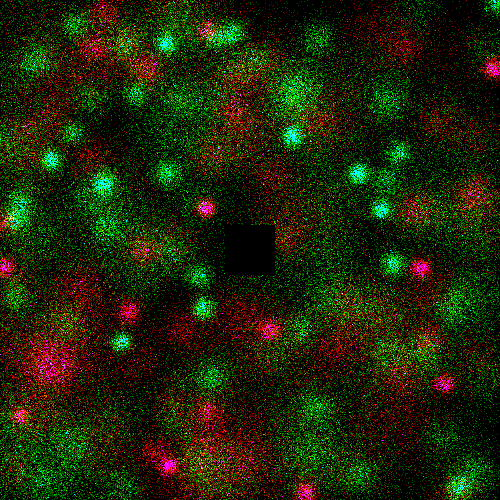
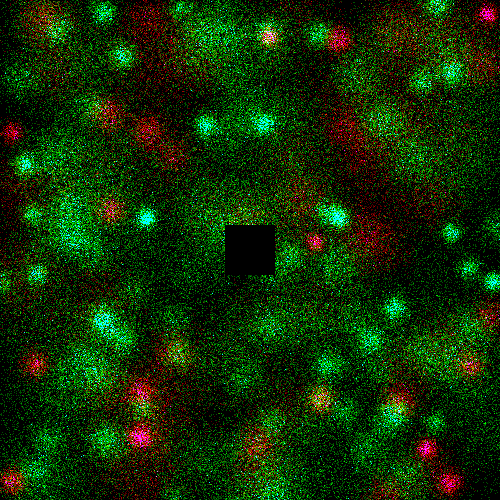
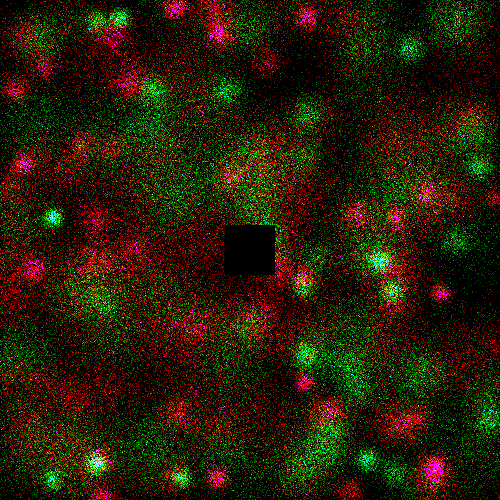
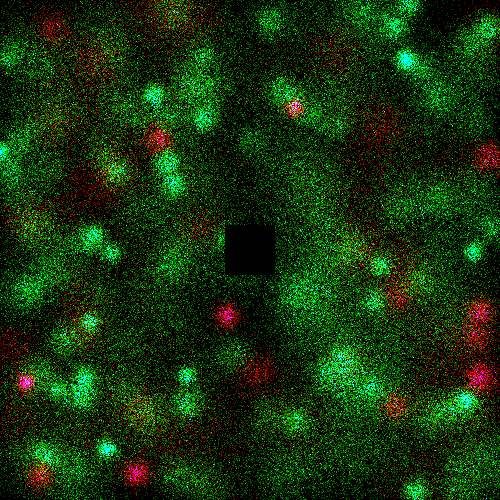
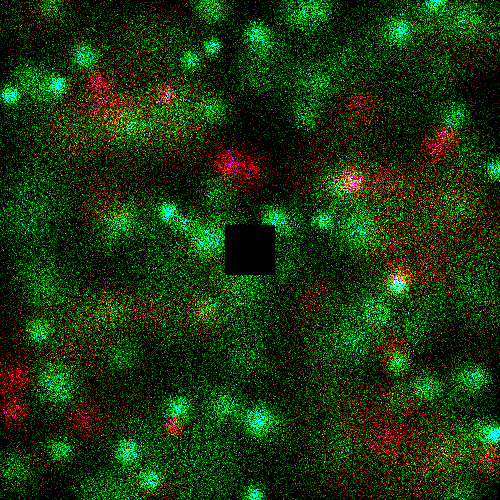
Problem Statement |
| | Introduction
You work for a company that has been given the contract to mine Mars for valuable resources not available here on earth. There are two minerals on mars that your company is interested in collecting, these will be refered to as A and B. When the Mars lander lands on the surface noOfRovers rovers are available to travel around the locality and collect minerals. Your job is to tell each of the rovers where to go to maximize the volume of usable minerals.
Input
Your method will be provided with the mineral concentrations mineralsA and mineralsB of minerals A and B respectivily in each square of a 1000 by 1000 grid. These will be provided in the form of arrays of 1,000,000 integers, which will represent the grid and will be provided in row major order. I.e. the first 1000 integer will represent the first row (y=0), the next 1000 the second row etc.. You will not be able to collect minerals from a square in centre of the grid between (450,450) and (550,550), inclusive, because your lander is in the way so this area will not contain any minerals in your input. Your rovers are equiped with a scoop and will collect any minerals within 10 units of the rover at any time including the end points of the segments formed by the waypoints.
Output
The lander will start in the middle of the map at grid reference 500, 500. You will be provided with noOfRovers rovers that each start at the lander and must return to the lander before they run out of fuel. Each rover is fuelled with enough fuel to travel a distance of 2000 units.
You need to provide a series of waypoints for each rover that plots a course around the map. Each waypoint will be the grid coordinates of the square you want the rover to travel to. The waypoints will be visited in the order they are given. The amount of fuel used up travelling betweem two waypoints is the Euclidean distance between those two waypoints.
Each waypoint should be in a seperate string in the returned array formatted as follows:
roverId x_coord y_coord
- roverId is the zero based index of the rover.
- x_coord and y_coord are between 0 and 999 inclusive
Mineral Concentrations
The mineral concentration at each point on the map is calculated from a collection of mineral pockets. The mineral pockets are only used to generate the mineral concentrations and are not provided to the competitors program. All random choices are chosen uniformly at random unless stated otherwise.
- The number of mineral pockets of type A is chosen between 50 and 250
- The number of mineral pockets of type B is 300 - (number of mineral pockets of type A)
- Each mineral pocket is placed randomly on the grid.
i.e x and y coordinates for the mineral pockets are chosen between 0 and 999 independantly.
- A standard deviation is chosen for each mineral pocket between 10 and 70 (the x and y deviations are identical).
- The number of mineral points in each mineral pocket is chosen between 2000 and 4000.
- Foreach of the mineral points:
- A grid point is chosen based on a Gaussian (normal) distribution with the mean and
standard deviation of the mineral pocket.
- The number of minerals of the type of the mineral pocket in that grid square is incremented by 1.
Scoring
Mineral A and B are required in equal quantity to be useful. So your score will be the minimum of the amounts collected, i.e.:
minimum(volume of mineral A delivered, volume of mineral B delivered)
If a rover does not return back to the lander craft before it runs out of fuel the minerals it has collected do not count towards your score.
Your final score will be the average of the scores on indivdual test cases.
Visualizer
As in past contests, a visualizer is provided.
|
| |
Definition |
| | | Class: | MarsRover | | Method: | generateWaypoints | | Parameters: | int, int[], int[] | | Returns: | String[] | | Method signature: | String[] generateWaypoints(int noOfRovers, int[] mineralA, int[] mineralB) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | Each grid square can only be collected once. If two rovers collect the same grid square only the first is counted. |
| - | If a rover does not return back to the lander craft (i.e. return to 500 500) before it runs out of fuel or fails to return to the lander then the minerals it has collected do not count towards your score and are wasted. |
| - | Your final score will be the average of your scores on indivdual test cases. |
| - | The minerals are all considered to be at grid points, while the rover follows a straight line between grid points. If a point (x,y) is within 10 units of a segment traversed by the rover, it is collected. |
| - | There are 100 test cases. |
| |
Constraints |
| - | You will be given between 5 and 10 rovers inclusive. |
| - | Each rover has 2000 units of fuel. |
| - | You can not return a total of more than 1000 waypoints for all rovers. I.e. your return array can not contain more than 1000 elements. |
| - | You will have 30 seconds of CPU time per testcase. |
| - | Your program can use up to 1024MB of memory. |
| |
Examples |
| 0) | |
| | | Returns:
"noOfRovers = 8
noOfMineralPockets of type A = 183
noOfMineralPockets of type B = 117
" | Red is type A, green is type B.
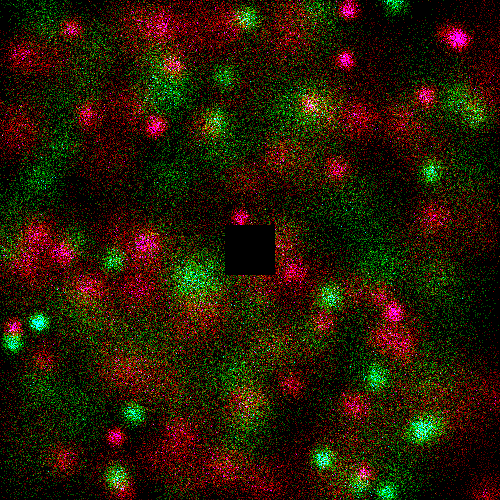 |
|
|
| 1) | |
| | | Returns:
"noOfRovers = 9
noOfMineralPockets of type A = 188
noOfMineralPockets of type B = 112
" | |
|
| 2) | |
| | | Returns:
"noOfRovers = 7
noOfMineralPockets of type A = 136
noOfMineralPockets of type B = 164
" | |
|
| 3) | |
| | | Returns:
"noOfRovers = 7
noOfMineralPockets of type A = 228
noOfMineralPockets of type B = 72
" | |
|
| 4) | |
| | | Returns:
"noOfRovers = 10
noOfMineralPockets of type A = 126
noOfMineralPockets of type B = 174
" | |
|
| 5) | |
| | | Returns:
"noOfRovers = 6
noOfMineralPockets of type A = 131
noOfMineralPockets of type B = 169
" | |
|
| 6) | |
| | | Returns:
"noOfRovers = 9
noOfMineralPockets of type A = 79
noOfMineralPockets of type B = 221
" | |
|
| 7) | |
| | | Returns:
"noOfRovers = 9
noOfMineralPockets of type A = 171
noOfMineralPockets of type B = 129
" | |
|
| 8) | |
| | | Returns:
"noOfRovers = 6
noOfMineralPockets of type A = 69
noOfMineralPockets of type B = 231
" | |
|
| 9) | |
| | | Returns:
"noOfRovers = 8
noOfMineralPockets of type A = 74
noOfMineralPockets of type B = 226
" | |
|