You have a sheet of paper and you are looking at it sideways. You can fold the paper exactly in half using one of the following operations:
-
Fold the right half of the paper counterclockwise over the left half.
-
Fold the right half of the paper clockwise under the left half.
The following picture illustrates the two possible folds:
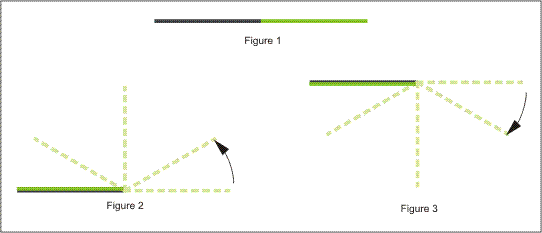
Figure 1 shows the original sheet of paper. Figure 2 shows the result of performing fold operation 1, and figure 3 shows the result of performing fold operation 2 (each on the original sheet of paper).
After one initial fold, the paper is two layers thick. You can continue folding the paper any number of times, and each time it will become twice as thick and half as long. The following picture shows one possible sequence of folds:
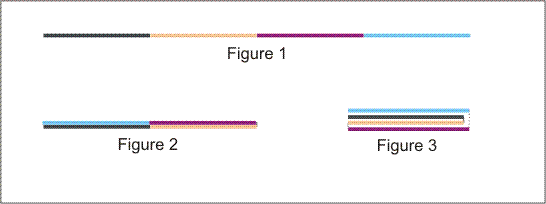
Figure 1 shows the original sheet of paper. Figure 2 shows the result of performing fold operation 1 on the original sheet. Figure 3 shows the result of performing fold operation 2 on the resulting two-layer sheet.
After some number of folds (possibly zero), you decide to unfold the paper. To do this, you simply work backwards and reverse each fold until you end up with the original sheet. Unfortunately, the paper will now show marks where each of the folds occurred. We go from left to right and label each mark where the paper bends slightly clockwise as an OUT, and each mark where the paper bends slightly counterclockwise as an IN. The following picture shows the unfolded version of the paper from the previous picture.
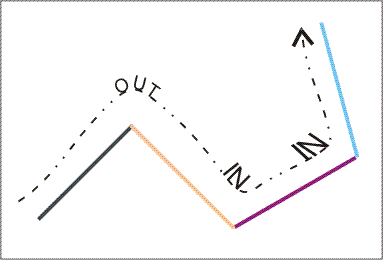
You are given a String[] code. Concatenate the elements of code to obtain one string. This string contains the marks on an unfolded sheet of paper from left to right, where '1' (one) represents an OUT and '0' (zero) represents an IN. So, for example, the paper in the picture above would be represented as "100". Return "YES" if code represents a piece of paper that could have been produced using the process described above, or "NO" otherwise (all quotes for clarity).
| 

