TopCoder problem "FrabonacciTree" used in TCCC07 Round 4 (Division I Level One)



Problem Statement

    

The 0-th and 1-st Frabonacci trees are each single nodes. For all i > 1, the i-th Frabonacci tree is constructed as follows:

  • Create a new node r. This will be the root node of the i-th Frabonacci tree.
  • Construct the (i-1)-th and (i-2)-th Frabonacci trees.
  • Attach the (i-2)-th Frabonacci tree as the left subtree of r.
  • Attach the (i-1)-th Frabonacci tree as the right subtree of r.
The number of vertices in Frabonacci trees grows very quickly, for example there are about 4*10^10 vertices in the 50-th Frabonacci tree.

To traverse a Frabonacci tree in preorder, perform the following operations:

  • Visit the root.
  • Traverse the left subtree.
  • Traverse the right subtree.
Let's traverse a Frabonacci tree and enumerate all vertices in the order of their visiting. There is the 3-rd Frabonacci tree with enumerated vertices on the picture.

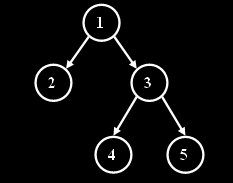
You are given three ints n, startIndex, finishIndex. Return the shortest route between the vertices startIndex and finishIndex in form of a String in the n-th Frabonacci tree. Each character of the result will be "L", "R" or "U", where "L" means a move to the left son, "R" means the move to the right son, and "U" means the move to the parent.

 

Definition

    
Class:FrabonacciTree
Method:shortestPath
Parameters:int, int, int
Returns:String
Method signature:String shortestPath(int n, int startIndex, int finishIndex)
(be sure your method is public)
    
 

Constraints

-n will be between 0 and 50, inclusive.
-startIndex will be between 1 and 1000000000, inclusive.
-finishIndex will be between 1 and 1000000000, inclusive.
-startIndex, finishIndex less or equal than the number of vertices in the n-th Frabonacci tree.
 

Examples

0)
    
3
2
4
Returns: "URL"
1)
    
3
4
2
Returns: "UUL"
2)
    
3
5
4
Returns: "UL"
3)
    
12
10
10
Returns: ""

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8149

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10924&pm=8149

Writer:

Mike Mirzayanov

Testers:

PabloGilberto , radeye , Olexiy , ivan_metelsky

Problem categories:

Recursion