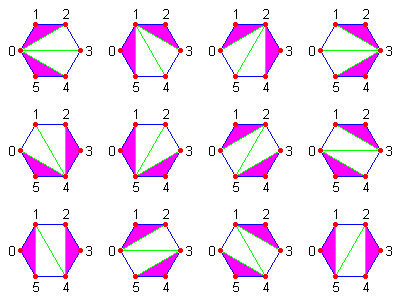
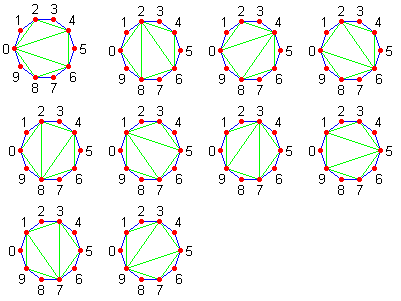
TopCoder problem "IsoscelesTriangulations" used in SRM 369 (Division II Level Three)



Problem Statement

    

Let's consider a regular polygon on the plane with n vertices, numbered from 0 to n-1, inclusive. The polygon's n-3 diagonals are called a triangulation if no two diagonals intersect at a point strictly inside the polygon. Two triangulations A and B are considered to be distinct if there are two vertices i and j such that A contains the diagonal between vertices i and j, and B doesn't contain this diagonal.

It's not hard to see that every triangulation breaks the polygon into n-2 triangles. The triangulation is called k-isosceles, if there are exactly k isosceles triangles among them. Given ints n and k, compute the number of distinct k-isosceles triangulations of a regular polygon with n vertices. Return the result modulo 123456789.

 

Definition

    
Class:IsoscelesTriangulations
Method:getCount
Parameters:int, int
Returns:int
Method signature:int getCount(int n, int k)
(be sure your method is public)
    
 

Notes

-A triangle is called isosceles if it has at least 2 sides with equal length.
-A regular polygon is a polygon which is equiangular (all angles are congruent) and equilateral (all sides have the same length).
-A diagonal is a line joining two nonadjacent vertices of a polygon.
 

Constraints

-n will be between 3 and 50, inclusive.
-k will be between 0 and n-2, inclusive.
 

Examples

0)
    
4
2
Returns: 2
We can have a diagonal between vertices 0 and 2 or between vertices 1 and 3. In both cases, there are 2 isosceles triangles.
1)
    
3
0
Returns: 0
The only triangulation of an equilateral triangle contains no diagonals and 1 isosceles triangle (the polygon itself).
2)
    
5
3
Returns: 5
A regular pentagon has 5 triangulations. Each of them is obtained by connecting one selected vertex with the two others that are not its neighbors, so each triangulation is 3-isosceles.
3)
    
6
2
Returns: 12

All 2-isosceles triangles of a regular hexagon are shown in the picture below. All isosceles triangles in each triangulation are colored purple.

4)
    
10
8
Returns: 10

All 8-isosceles triangulations of a regular 10-gon are shown in the picture below. All triangles in each triangulation are isosceles.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8179

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10785&pm=8179

Writer:

ivan_metelsky

Testers:

PabloGilberto , Yarin , Olexiy

Problem categories:

Dynamic Programming