Problem Statement |
| |
A polyline is a sequence of line segments such that each segment starts at the point where the previous segment ended.
If two polylines have a common point, we say that they belong to the same picture.
The common point does not have to be an endpoint of a line segment.
Your method will be given a String[] polylines. Concatenate the elements of polylines to get a space-separated list of polyline descriptions.
Each polyline description consists of one or more point descriptions, separated by single dashes ('-'). Each point is described by its two non-negative integer coordinates,
separated by a comma (',').
Return the number of pictures in the union of all the given polylines.
|
| |
Definition |
| | | Class: | PolylineUnion | | Method: | countComponents | | Parameters: | String[] | | Returns: | int | | Method signature: | int countComponents(String[] polylines) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The point sequence that defines a polyline may contain the same point more than once, and even consecutive points are allowed to be equal. |
| - | A polyline may be just a single point. |
| |
Constraints |
| - | polylines will have the format described in the problem statement. |
| - | polylines will contain between 1 and 50 elements, inclusive. |
| - | Each of the elements in polylines will contain between 0 and 50 characters, inclusive. |
| - | Each coordinate of each point specified in polylines will be between 0 and 10000, inclusive. |
| - | The point coordinates in polylines will not contain unnecessary leading zeros. |
| |
Examples |
| 0) | |
| | | Returns: 1 | Two intersecting line segments form a single picture.
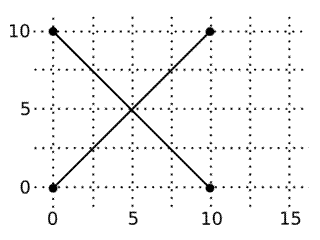
|
|
|
| 1) | |
| | {"0,0-10,5 5,0-15,5-10,10-5,5"} |
| Returns: 2 | Two non-intersecting polylines.
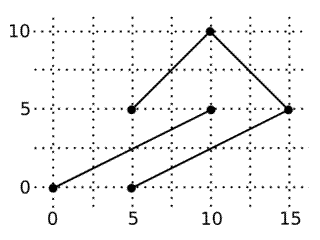
|
|
|
| 2) | |
| | | Returns: 2 | | Note that you first have to concatenate the elements of polylines and only then parse the resulting string. |
|
|
| 3) | |
| | {"10,0-10,1-9,2-9,3-8,4 ","8,2-9,2-10,3 ","12,2-11,2-9,1"} |
| Returns: 1 | Together, these three polylines form a single picture. From a graph theoretical point of view, this picture can be seen as a tree with 11 vertices. (Ten of them are the given points and one is the intersection of 10,1-9,2 and 11,2-9,1.)
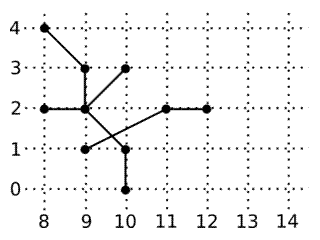
|
|
|
| 4) | |
| | {"0,0-10,0-0,0 20,0-8,0-20,0"} |
| Returns: 1 | | The union of these two polylines is the line segment 0,0-20,0. |
|
|
| 5) | |
| | {"1,1 2,2 3,3 4,4 3,3-4,4"} |
| Returns: 3 | | A single point is a special case of a polyline. |
|
|
| 6) | |
| | {"10,10-20,10 20,10-15,18 15,18-10,10"} |
| Returns: 1 | |
|
| 7) | |
| | |


