In this task we will consider a mechanical puzzle that has the shape of a regular tetrahedron.
Each edge is divided into edgeLength unit segments, and each face is divided into
unit equilateral triangles.
See the picture below for an example of a puzzle with edgeLength=3.
On the real puzzle each of the small triangles is colored using one of four
colors (red, green, blue, and yellow).
The colors will not matter in this problem,
but we will still use them in the pictures.
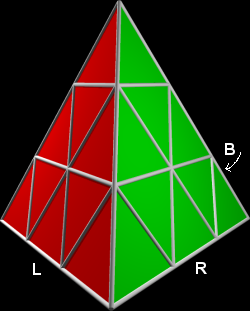
Little Juliet is playing with the puzzle. Initially, she placed the puzzle on the table before her
so that it was lying on one of its sides. Then she rotated it so that one vertex pointed towards her.
This position of the pyramid will be called the canonical position. When a pyramid is in the
canonical position, we can label the three edges of the bottom face as L (front left), R (front right)
and B (back), as in the picture above.
Little Juliet performed a sequence of moves, which left the puzzle in a scrambled state.
Each of the moves was of one of these types:
- "+X": Rotate the top X rows of the pyramid 120 degrees counter-clockwise (seen from above).
- "-X": Rotate the top X rows of the pyramid 120 degrees clockwise.
- "L": Flip the entire puzzle around the front left edge. The face that was previously the front left face is now the bottom face. Rotate the puzzle 60 degrees counter-clockwise and translate it back into the canonical position.
- "R": Flip the entire puzzle around the front right edge, rotate it 60 degrees counter-clockwise and translate it back into the canonical position.
- "B": Flip the entire puzzle around the back edge, rotate it 60 degrees counter-clockwise and translate it back into the canonical position.
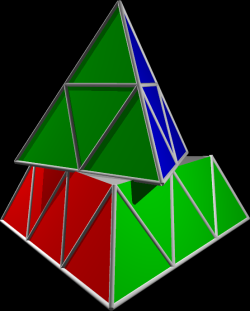
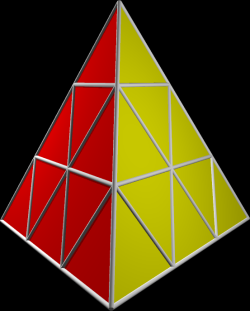
The pictures above show the results of some of the moves, each starting with a puzzle in the canonical position, with the entire front left side being red, front right side green, back side blue and bottom side yellow.
The first picture is an almost finished move -2. The second picture is the result of the move B (the bottom side is now blue).
After seeing the scrambled puzzle, Juliet began to wonder whether repeating the exact same sequence of moves over and over again would bring it back to the initial state -- that is, each of the small triangles must return to the exact same place where it started.
You are given an int edgeLength and a String[] moves. Concatenate the elements
of moves to get a space-separated list of moves Juliet performed.
If there is a positive integer K such that performing all the moves exactly K times brings each small triangle to the place where it was in the beginning, find the smallest such K and return the value (K mod 987654319). If no such K exists, return -1.
| 

