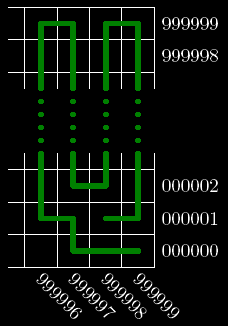
TopCoder problem "DukeOnLargeChessBoard" used in SRM 375 (Division I Level Three)



Problem Statement

    

Let's define a duke as a chess figure that is only allowed to move 1 cell up, down, left or right.

Let's consider a large chess board of size 1000000×1000000. Both rows and columns are numbered from "000000" to "999999". A cell is labeled as "(<Column number>, <Row number>)" (quotes for clarity), where <Column number> and <Row number> each contain exactly six digits. For example, "(499999, 000000)" and "(500000, 000000)" are the two cells in the middle of the bottom row.

A duke is placed on a chessboard in the cell initPosition.

Let's describe a duke's path as a space-separated list of cells visited by the duke. For example, "(444444, 600000) (444445, 600000) (444445, 599999)" is a path consisting of two moves. The first move is one cell to the right and the second move is one cell down.

A path is called simple if it contains no repeated cells.

Consider the lexicographically greatest simple path of a duke starting in initPosition. Return the last cell of this path in the same format as initPosition.

 

Definition

    
Class:DukeOnLargeChessBoard
Method:lastCell
Parameters:String
Returns:String
Method signature:String lastCell(String initPosition)
(be sure your method is public)
    
 

Notes

-A String A is greater than a String B lexicographically if B is a proper prefix of A, or if A has a greater character at the first position where the strings differ.
 

Constraints

-initPosition will contain exactly 16 characters.
-initPosition will be a valid notation of a cell inside the board.
 

Examples

0)
    
"(999999, 999999)"
Returns: "(000000, 999999)"
The duke is located in the upper right corner. First he goes all the way down to (999999, 000000). Then he has to move one cell left and then goes all the way up. Again, one move left and all the way down. This snake-like pattern covers the entire board and finishes in the left-most row, where the duke moves up until he stops in the upper-left corner of the board, which is (000000, 999999).
1)
    
"(999999, 000000)"
Returns: "(000000, 000000)"
If a duke starts in the lower-right corner of the board, he will also follow a snake-like pattern. This time, he takes odd columns up and even columns down. In the end he will move down the 000000 column and finish his path in (000000, 000000).
2)
    
"(000000, 999998)"
Returns: "(000000, 999999)"
The duke will visit only 2000000 cells on his path if he starts from this point. First he will move all the way right to (999999, 999998), then one cell up to (999999, 999999) and all the way left to (000000, 999999). In this cell we will have no unvisited neighbors to move into.
3)
    
"(999998, 000001)"
Returns: "(999999, 000000)"
4)
    
"(123456, 235711)"
Returns: "(000000, 112256)"
5)
    
"(987654, 123456)"
Returns: "(864197, 000000)"

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8317

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=10794&pm=8317

Writer:

darnley

Testers:

PabloGilberto , Olexiy , ivan_metelsky , ged

Problem categories:

Greedy