Problem Statement |
| | You are given a convex polygon and you must count the number of N-cool points. A point is N-cool if it is a lattice point covered by the polygon and also an endpoint of some N-cool segment. A line segment is N-cool if it contains at least N lattice points that are covered by the polygon. A point is considered covered by the polygon if it is inside or on the boundary of the polygon. Endpoints of a segment are considered to be inside of it. A lattice point is a point with integer coordinates.
Consider the example in the picture below. Here N is equal to 6, and there are 21 6-cool points, marked green. Also two 6-cool segments, which are colored red, are shown.
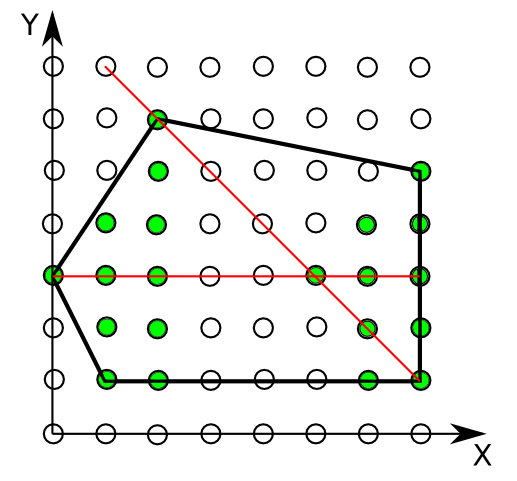
You are given int[]s x and y describing the vertices of the polygon (in no particular order). The coordinates of each vertex are specified by corresponding elements of x and y. Return the number of N-cool points.
|
| |
Definition |
| | | Class: | NCool | | Method: | nCoolPoints | | Parameters: | int[], int[], int | | Returns: | int | | Method signature: | int nCoolPoints(int[] x, int[] y, int n) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | A polygon is convex if it contains all the line segments connecting any pair of its points. |
| |
Constraints |
| - | x and y will each contain between 3 and 50 elements, inclusive. |
| - | x and y will contain the same number of elements. |
| - | All elements of x and y will be between 0 and 10000, inclusive. |
| - | The number of lattice points inside or on the boundary of the specified polygon will not be greater than 500000. |
| - | N will be between 2 and 500000, inclusive. |
| - | The polygon specified by x and y will be convex and will have nonzero area. |
| |
Examples |
| 0) | |
| | {0, 1, 2, 7, 7} | {3, 1, 6, 1, 5} | 6 |
| Returns: 21 | | This is the example from the problem statement. |
|
|
| 1) | |
| | | Returns: 3 | | These three points form a triangle, whose sides are 2-cool segments, so all three vertices are 2-cool. |
|
|
| 2) | |
| | {0, 0, 1, 2, 2, 1, 0, 0, 2} | {0, 1, 2, 2, 1, 0, 0, 0, 2} | 3 |
| Returns: 6 | | One point can be mentioned in the input two or more times. |
|
|
| 3) | |
| | {0, 1, 1, 2, 2, 3, 3, 4, 4, 5} | {1, 0, 2, 0, 2, 0, 2, 0, 2, 1} | 5 |
| Returns: 4 | | There can be 3 points of the polygon, lying on the same line. |
|
|
| 4) | |
| | {0, 1, 1, 2, 2, 3, 3, 4, 4, 5} | {1, 0, 2, 0, 2, 0, 2, 0, 2, 1} | 4 |
| Returns: 10 | |
|
