Problem Statement |
| | At our company, the hard drive capacity of the file servers is very small, which forces the administrators to delete files frequently to recover hard disk space. Some time ago, they used the operating system interface to traverse the file system from the root directory to the files, deleting big old files in the process.
The file system is structured as a rooted tree, specified by parent, size and type. The ID of a node is its 0-based position inside parent. For example, the 3rd node has ID=3. The k-th node is a file if type[k] is 'F' and is a directory if type[k] is 'D'. The parent of the k-th node is the parent[k]-th node, which is guaranteed to be a directory. The tree's root is node 0 and its parent is -1, indicating that it is not contained inside any other node. Finally, if the k-th node is a file, its size is size[k]; if the k-th node is a directory, size[k] will be equal to the sum of the sizes of its immediate child nodes.
Last week, a graphical interface to look at the entire file system at once was released. In this interface, a rectangle of width x height units with its lower-left corner at (0,0) and its upper-right corner at (width, height) is split horizontally between directories and files contained by the root directory. Then, each root's subdirectory is split vertically between its children, and so on, switching the split direction at each level. To split a rectangle horizontally, split its width between its children proportionally to their sizes, ordering the children left to right in increasing order by ID. To split a rectangle vertically, split its height between its children proportionally to their sizes, ordering the children from bottom to top in increasing order by ID.
For example, given the following file system structure (see example 0):
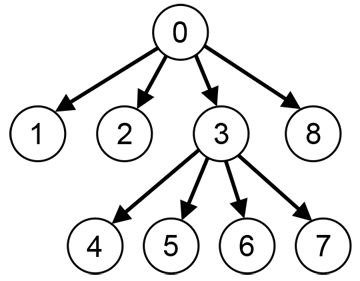
Then, given the blue rectangle with width=20 and height=8, the root node divides it between all its children, giving the directory 3 a bigger part because its total size is greater than the files 1, 2 and 8. This division is made horizontally, where the x axis goes from left to right. This division can be seen in the following image:
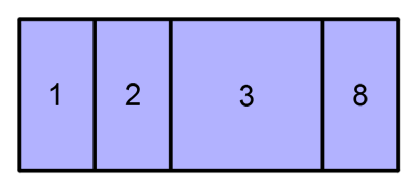
Then, the directory 3 divides its red rectangle between its children, ordering them from bottom to top in increasing order by ID. This division is made vertically, where the y axis goes from bottom to top. This division can be seen in the following image:
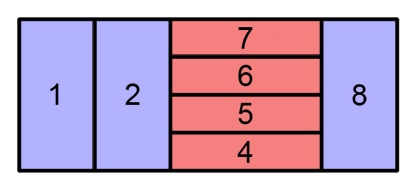
When an administrator clicks a file's rectangle, the file is erased and the rectangles are recalculated. Given the position of many clicks made by an administrator, return a int[] with the same number of elements as px, where the k-th element is the ID of the file erased by the click made at (px[k], py[k]). It is guaranteed that the administrator always clicks strictly inside some file's rectangle.
|
| |
Definition |
| | | Class: | TreeMaps | | Method: | eraseFiles | | Parameters: | String, int[], int[], int, int, int[], int[] | | Returns: | int[] | | Method signature: | int[] eraseFiles(String type, int[] parent, int[] size, int width, int height, int[] px, int[] py) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | type will contain N elements, where N is between 2 and 50, inclusive. |
| - | Each character of type will be either 'F' or 'D'. |
| - | At least one character in type will be 'F'. |
| - | The first character of type will be 'D'. |
| - | parent will contain exactly N elements. |
| - | Each element of parent will be between 0 and N-1, inclusive, except for the first element which will be equal to -1. |
| - | Each node that appears in parent will be a directory. |
| - | The structure defined by parent will be a rooted tree at 0. This means that there will be no cycles and all nodes can reach the root by following the parent links. |
| - | size will contain exactly N elements. |
| - | Each element of size will be between 1 and 1000, inclusive. |
| - | Each element of size where the corresponding element of type is 'D' will be equal to the sum of the sizes of its children. |
| - | width will between 2 and 1000, inclusive. |
| - | height will between 2 and 1000, inclusive. |
| - | px will contain M elements, where M is between 1 and the number of 'F's in type, inclusive. |
| - | Each element of px will be between 0 and width, exclusive. |
| - | py will contain exactly M elements. |
| - | Each element of py will be between 0 and height, exclusive. |
| - | There will be no k such that the point (px[k], py[k]) lies at a distance less than 1E-6 from a file rectangle's border. |
| |
Examples |
| 0) | |
| | "DFFDFFFFF" | {-1, 0, 0, 0, 3, 3, 3, 3, 0} | {10, 2, 2, 4, 1, 1, 1, 1, 2} | 20 | 8 | {12, 12} | {1, 4} |
| Returns: {4, 6 } | | The file system structure and the initial division of this example can be seen in the problem statement. Observe that after erasing file 4 with the first click, the image is recalculated and the point (12,4) is not in a rectangle's boundary anymore. |
|
|
| 1) | |
| | "DFFDFFFFF" | {-1, 0, 0, 0, 3, 3, 3, 3, 0} | {10, 2, 2, 4, 1, 1, 1, 1, 2} | 20 | 8 | {12, 12, 12, 12, 12} | {1, 1, 1, 1, 1} |
| Returns: {4, 5, 6, 7, 2 } | | The file system structure and the initial division of this example can be seen in the problem statement. The first four clicks erase all the files in directory 3. Note that after clearing a directory, the system gives it no area, so the fifth click erases file 2. |
|
|
| 2) | |
| | "DDDFFDFFF" | {-1, 0, 0, 1, 1, 2, 2, 5, 5} | {10, 4, 6, 2, 2, 5, 1, 2, 3} | 50 | 50 | {16, 41, 32} | {10, 38, 29} |
| Returns: {3, 8, 7 } | |
|
| 3) | |
| | "DFFFFD" | {-1, 5, 5, 5, 5, 0} | {10, 4, 2, 3, 1, 10} | 20 | 20 | {1, 1} | {2, 18} |
| Returns: {1, 4 } | |
|


