Problem Statement |
| | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
An N-segment display is a set of N on/off display elements (segments), positioned in such a way that certain arrangements of elements being on and off lead to symbols being represented in the display. Common examples of these types of display are 7-segment displays, which can display arabic numeral digits and 14- or 16-segment displays which can display alphanumeric symbols. See the diagram below for an example of a 7-segment display and its representation of the digits from 0 to 9.
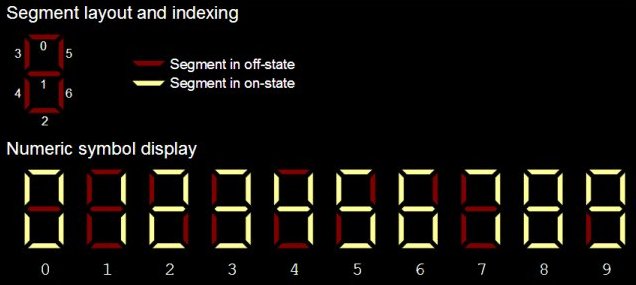
You suspect that certain segments in a particular N-segment display are broken and it is therefore not displaying symbols properly. If a segment is broken, then it remains permanently in an off state, even if the symbol being displayed requires that it turn on. Otherwise, if the segment is working, it will be on when the symbol being displayed requires it to be on and off otherwise. You want to know which segments are broken, so you observe the display for a period of time and note the patterns it displays. The display is set up to only ever show symbols from a known set, but you don't know what symbols from that set might be displayed or in what order they might be appear. Your task is to identify which segments of the display are working and which of them are broken.
You are given the set of symbols that the display shows as a String[], where each element describes a single symbol. Character j in element i will be '1' if segment j of the display should be on when symbol i is being displayed and '0' if it should be off. You are given the patterns that you observed being displayed in a String[] patterns, where each element describes a single pattern that you observe in the display. Character j of element i is '1' if segment j of the display is on for pattern i and '0' if it is off. Return a String containing exactly N elements. Character j of the return should be 'Y' if segment j of the display is definitely working, 'N' if segment j is definitely broken and '?' if there is no way of determining whether or not it is broken from the given data. If there is no way of interpreting the data consistent with some subset of the segments being broken, return "INCONSISTENT" (quotes for clarity) instead. |
| |
Definition |
| | | Class: | NSegmentDisplay | | Method: | brokenSegments | | Parameters: | String[], String[] | | Returns: | String | | Method signature: | String brokenSegments(String[] symbols, String[] patterns) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | A segment can be considered definitely to be working, if no configuration exists, consistent with the described behavior, in which it is broken. |
| - | A segment can be considered definitely to be broken, if no configuration exists, consistent with the described behavior, in which it is working. |
| - | If neither of the above conditions is true for a segment, there is no way of being sure whether it is broken or not. |
| |
Constraints |
| - | patterns and symbols will each contain between 1 and 50 elements, inclusive. |
| - | Each element of patterns and symbols will contain between 1 and 50 characters, inclusive. |
| - | Each element of patterns and symbols will contain the same number of characters. |
| - | Each character in patterns and symbols will be '1' (one) or '0' (zero). |
| |
Examples |
| 0) | |
| | {"1011111","0000011","1110110","1110011","0101011"
,"1111001","1111101","1000011","1111111","1111011"} | {"1011111"} |
| Returns: "Y?YYYYY" | This test case represents the 7-segment display shown in the problem statement. The display shows only the numeric symbols given in the statement. The only symbol observed in the display is

This could be either '0' or '8', so there is no way of telling whether segment 1 is broken or not. |
|
|
| 1) | |
| | {"1011111","0000011","1110110","1110011","0101011"
,"1111001","1111101","1000011","1111111","1111011"} | {"0111111"} |
| Returns: "NYYYYYY" | Now the symbol being shown is

This can only be '8', so segment 0 must be broken. |
|
|
| 2) | |
| | {"1011111","0000011","1110110","1110011","0101011"
,"1111001","1111101","1000011","1111111","1111011"} | {"1000000","0010000"} |
| Returns: "INCONSISTENT" | 
There is no way that the observed symbols can be consistent with the set that the display can show. |
|
|
| 3) | |
| | {"1011111","0000011","1110110","1110011","0101011"
,"1111001","1111101","1000011","1111111","1111011"} | {"0010110","0010010","0010000"} |
| Returns: "NNYNYYN" | 
We can deduce that segments 0, 1, 3 and 6 are broken. |
|
|
| 4) | |
| | {"110000111001","100000101000","000001010000"
,"101100010011","111111111101"} | {"010000000000","010000000000","000000000000"
,"000000000000","000000000000"} |
| Returns: "NY????NNN??N" | |
|
| 5) | |
| | {"00000000001000000010","01010000001011101110"
,"01010101110110011010","00111001111001000100"
,"10010111010110110000","11011011001000110001"} | {"00011000010000000000","10010110010000100000"
,"00010100010000001000","00010100010000001000"
,"00010000000000101000","00000000000000000000"
,"00010100010000001000","00011000010000000000"
,"00011000010000000000","00000000000000000000"} |
| Returns: "YNNYYYYNNYNNNNYNYNN?" | |
|
| 6) | |
| | {"001000111101000","000001111011001"
,"010010100100010","111000100010011"
,"011011011010001","010011111101000"
,"000101011110011","010000011111000"
,"000001100100011","000000111110000"} | {"001000110001000","000101110000011"
,"000101010000011","001000110101000"
,"010001100000111"} |
| Returns: "INCONSISTENT" | |
|




