TopCoder problem "SnakesOnAPlane" used in TCO08 Championship (Division I Level Three)



Problem Statement

    

NOTE: This problem contains images that may not be displayed properly if viewed outside the contest applet.

The Cartesian plane is covered with snakes. You will be given a rectangular portion of the plane, divided into a grid of squares. Each square will either contain a segment of a snake or a barrier.

Each snake occupies a chain of adjacent squares, connected horizontally and/or vertically. Snakes are at least 2 segments long (one segment per square) and cannot overlap each other or themselves. Each snake must meet at least one of the following two conditions (see the figures below for examples):

  1. Both endpoints must be in squares on the edge of the rectangle.
  2. Both endpoints must be horizontally or vertically adjacent to each other, and the snake is at least 4 segments long (so the snake forms a loop).

The portion of the plane will be given as a String grid, where each character represents one square. A '#' represents a barrier and a '.' (period) represents a square that contains a segment of a snake. Fill the grid with snakes so that all of the non-barrier squares are filled. Do this in such a way that minimizes n, the number of snakes whose endpoints are not adjacent (and therefore, must be on the edge of the grid). Return n, or return -1 if there is no way to fill every non-barrier square.

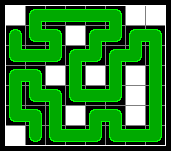
For example, the grid defined by the following input: 


    { "......",
      ".#.##.",
      ".#....",
      "....#.",
      ".##.#.",
      "......" }

can be filled with snakes in several ways and a few are shown in the figures below:



In each figure, there are 2 snakes that do not form a loop. There is no way to fill the grid with only 1, so 2 is the correct answer for this input.

 

Definition

    
Class:SnakesOnAPlane
Method:snakes
Parameters:String[]
Returns:int
Method signature:int snakes(String[] grid)
(be sure your method is public)
    
 

Constraints

-grid will contain between 1 and 12 elements, inclusive.
-Each element of grid will contain the same number of characters, between 1 and 12, inclusive.
-Each element of grid will contain only the characters '#' and '.' (period).
 

Examples

0)
    
{ "......",
  ".#.##.",
  ".#....",
  "....#.",
  ".##.#.",
  "......" }
Returns: 2
This is the example from the problem statement.
1)
    
{ "###.###",
  "###.###",
  ".......",
  "###.###",
  "###.###" }
Returns: -1
This grid cannot be filled without two snakes overlapping.
2)
    
{ "#.....##",
  "...#....",
  "........",
  "..#.#.#.",
  "......#.",
  "...#..#.",
  "#......." }

Returns: 1
This grid can be filled by a single snake, as shown in this figure:
3)
    
{ "###########",
  "#......#...",
  "#.####.#...",
  "#.#..#.####",
  "#.#..#.####",
  "#.####.#..#",
  "#......#..#",
  "###########" }
Returns: 0
This grid can be completely filled with 4 snakes that form a loop. You do not need to count these, so the answer is 0.
4)
    
{ "####.######",
  "#.........#",
  "..........#",
  "#..........",
  "#.........#",
  "#####.#####" }

Returns: -1
5)
    
{ "##",
  "#." }

Returns: -1
Snakes must be at least 2 segments long.
6)
    
{ ".", "." }
Returns: 1
7)
    
{ "#" }
Returns: 0

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=8603

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=12019&pm=8603

Writer:

legakis

Testers:

PabloGilberto , Olexiy , Andrew_Lazarev , ivan_metelsky

Problem categories:

Dynamic Programming