Problem Statement |
| | Dissatisfied with the inconvenient spherical shape of the Earth, a group of
map-makers have gone to Magrathea to obtain a custom-built planet. They
decided to design their new planet to be flat and in the shape of a polygon.
All coordinates will be in the Cartesian (x, y) plane.
In order to provide everyone on the planet with internet access, a wireless
router will be placed at every lattice point that is inside the polygon (a
lattice point is a point with integer coordinates). The map-makers decided to
keep their job simple by choosing a polygon with no lattice points on its
boundary.
Because the map-makers are highly rational people, they decided that the coordinates of all the
vertices of the polygon would be fractions with a common denominator. The vertices of the
polygon (in order), are given by the int[]s x and y, and by the
common denominator denom. The ith vertex is
(x[i]/denom, y[i]/denom).
Calculate and return the number of routers required.
|
| |
Definition |
| | | Class: | WifiPlanet | | Method: | routersNeeded | | Parameters: | int[], int[], int | | Returns: | long | | Method signature: | long routersNeeded(int[] x, int[] y, int denom) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | x and y will contain the same number of elements. |
| - | x and y will each contain between 3 and 50 elements, inclusive. |
| - | Each element of x and y will be between 1 and 10^9, inclusive. |
| - | No two vertices of the polygon will be the same. |
| - | No two edges of the polygon (including their end-points) will intersect, with the exception that adjacent edges will intersect at their common end-point. |
| - | No lattice point will lie on the boundary of the polygon. |
| - | denom will be between 2 and 10^9, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 2 | This is illustrated in the image below:
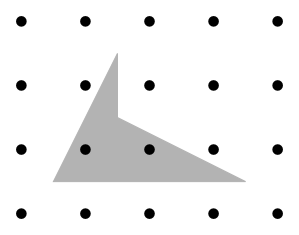
|
|
|
| 1) | |
| | {3,3,4,4,5,6,10,10,11,11,10,10,9,9} | {1,2,2,6,3,8,8,9,9,3,3,2,2,1} | 3 |
| Returns: 4 | |
|
| 2) | |
| | {50,1000050,1000049} | {2,1000002,1000003} | 100 |
| Returns: 0 | |
|
| 3) | |
| | {32,32,64,8,15,1000,999} | {1,10,10,48,48,47,1} | 16 |
| Returns: 120 | |
|
| 4) | |
| | {1,1000000000,1000000000,1} | {1,1,1000000000,1000000000} | 3 |
| Returns: 111111110888888889 | |
|