Problem Statement |
| |
Little John has found a set of stairs where each stair might contain a number of sweets.
He wants to collect as many of these sweets as possible.
Each stair can be described as a line segment in the Cartesian plane parallel to the x-axis and
having a positive y-coordinate. These segments don't overlap and don't have common endpoints.
When John is on a stair, he can move freely between its two endpoints and can collect all sweets on it.
He can jump from a point on one stair to a point on another stair (including endpoints of stairs) if
the Euclidean distance between them is less than or equal to K. He can only jump to stairs
where the y-coordinate is greater than or equal to his current y-coordinate.
You are given a int[] sweets, the i-th element of which is the number
of sweets on the i-th stair. You are also given int[]s x, y
and stairLength. The coordinates of the leftmost point of the i-th stair are
(x[i], y[i]) and the horizontal length of that stair is stairLength[i].
John starts at point (0, 0) and can move wherever he wants along the x-axis before making his first jump.
He can first jump to any point on any stair (including endpoints of stairs) as long as the Euclidean
distance between the initial and the final points of the jump does not exceed K.
Return the maximum possible number of sweets he can collect.
|
| |
Definition |
| | | Class: | GetToTheTop | | Method: | collectSweets | | Parameters: | int, int[], int[], int[], int[] | | Returns: | int | | Method signature: | int collectSweets(int K, int[] sweets, int[] x, int[] y, int[] stairLength) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The Euclidean distance between points (x1, y1) and (x2, y2) is equal to the square root of (x1 - x2)^2 + (y1 - y2)^2. |
| |
Constraints |
| - | K will be between 1 and 10000, inclusive. |
| - | sweets will contain between 1 and 50 elements, inclusive. |
| - | sweets, x, y and stairLength will all contain the same number of elements. |
| - | Each element of sweets will be between 0 and 9999, inclusive. |
| - | Each element of x will be between 1 and 10000, inclusive. |
| - | Each element of y will be between 1 and 10000, inclusive. |
| - | Each element of stairLength will be between 1 and 1000, inclusive. |
| - | No stairs will overlap or share endpoints. More formally, for each i and j, where y[i] is equal to y[j], either x[i] + stairLength[i] will be less than x[j] or x[j] + stairLength[j] will be less than x[i]. |
| |
Examples |
| 0) | |
| | 2 | {1, 2, 3, 4, 3, 5} | {1, 1, 1, 4, 5, 5} | {1, 3, 4, 1, 2, 3} | {2, 1, 1, 2, 1, 1} |
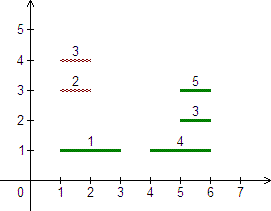
| Returns: 13 | From the start position (0, 0) John can jump on stair 0 (all stair indices are 0-based) and collect 1 sweet. Then he can move to the rightmost point of this stair and jump on stair 3 (the one with the leftmost coordinate (4, 1)).
There he collects 4 sweets. Now he has two options:
- go back to stair 0, jump on stair 1 to collect 2 sweets and then jump on stair 2 to collect 3 sweets;
- jump from stair 3 to stair 4 to collect 3 sweets and then to stair 5 to collect 5 sweets.
Obviously the second option gives more sweets, so he will choose it and collect 1+4+3+5=13 sweets.
 |
|
|
| 1) | |
| | 4 | {2, 8, 7, 4, 1, 4, 7, 5, 11, 4} | {2, 9, 4, 6, 10, 5, 2, 8, 1, 10} | {1, 1, 3, 3, 3, 5, 6, 6, 8, 9} | {2, 2, 1, 2, 2, 2, 4, 3, 2, 2} |
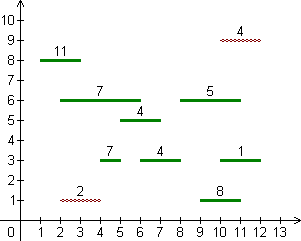
| Returns: 47 | John can make his first jump on stair 0 or on stair 1 (all stair indices are 0-based). Both choices allow him to visit the same set of stairs afterwards. It is better to jump on stair 1, because it contains 8 sweets. Then he can visit stairs 2, 3, ..., 7 collecting 1+4+7+4+7+5=28 sweets. Finally, he should choose between stairs 8 and 9. Stair 8 contains more sweets, so he will jump on it and collect 11 more sweets.
 |
|
|
| 2) | |
| | 10 | {1, 3, 5, 7} | {1, 6, 2, 8} | {2, 4, 1, 2} | {4, 1, 7, 4} |
| Returns: 16 | |
|
| 3) | |
| | 3 | {80, 20, 15, 13, 10, 7, 8, 9, 1, 4, 3, 15, 14, 19, 22, 12, 6, 15, 10, 30, 1, 1} | {2, 8, 11, 17, 20, 14, 10, 16, 8, 14, 19, 6, 6, 6, 6, 15, 15, 15, 14, 20, 20, 20} | {1, 2, 3, 2, 1, 4, 6, 7, 8, 8, 8, 9, 10, 11, 12, 9, 10, 11, 12, 9, 10, 11} | {2, 2, 2, 2, 2, 2, 3, 2, 3, 2, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1} |
| Returns: 129 | |
|
| 4) | |
| | 10 | {0, 10, 11, 2, 0} | {1, 26, 29, 22, 3} | {1, 83, 88, 22, 5} | {11, 1, 23, 15, 8} |
| Returns: 0 | | John can not collect any sweets. |
|
|
| 5) | |
| | 5 | {2, 0, 5} | {1, 8, 9} | {6, 6, 1} | {3, 6, 3} |
| Returns: 7 | |
|
| 6) | |
| | 2 | {2, 9, 9, 1, 9, 9, 8} | {10, 8, 6, 6, 8, 7, 3} | {6, 7, 5, 4, 5, 2, 5} | {1, 1, 1, 1, 1, 1, 1} |
| Returns: 47 | |
|

