There are several cities in a country, and some pairs of those cities are connected by one-way roads (although it is possible that there are one-way roads both from A to B and from B to A). It is possible to get from any city to any other city using roads. A traveler starts from some city, and travels along one of the roads every day. A number x is called vacation-friendly if a traveler can have an x-day long vacation. That means he can start from some city, travel exactly x roads, and be back at the city where he started.
A vacation string is an infinite string of '0' and '1' digits, which has a '1' in the x-th (1-based) position if and only if x is a vacation-friendly number.
For example, consider the country shown in the following picture.
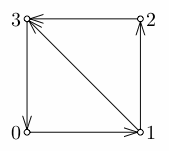
Its vacation string is "0011011111111...": 0->1->3->0 is a 3-day vacation, 0->1->2->3->0 is a 4-day vacation, 0->1->3->0->1->3->0 is a 6-day vacation, 0->1->2->3->0->1->3->0 is a 7-day vacation, and so on.
It turns out that every vacation string becomes periodic at some point. We will enclose the period in parentheses to obtain a finite representation for a vacation string. For example, the above vacation string can be represented by "00110(1)" or "00110111(11)". We will call the shortest possible representation canonical.
Given a description of a country as a String[] arcs, where the j-th character of the i-th element of arcs is 'Y' if there is a road from city i to city j, and 'N' otherwise, return the canonical representation of its vacation string. | 