Russian Checkers is a game played on an 8x8 board of alternating dark and light squares. The square in the lower-left corner is dark, and only dark squares are used in the game. Columns are labelled 'a' to 'h' from left to right, and rows are labelled '1' to '8' from bottom to top. Each cell is denoted by its column followed by its row (for example, "a4" or "f8"). The following image shows an empty board:

There are two players taking alternate turns. One player controls the white pieces and the other controls the black. The white player sits at the bottom of the board and the black player sits at the top. Every piece is exactly in one of the two types: "man" and "king".
There are two types of moves - a simple move and a capturing move. The player can make a simple move in his turn only if there are no available capturing moves for him in this turn.
A simple move for a "man" consists of moving diagonally forward to an adjacent empty square. White pieces move forward by moving to higher numbered rows, and black pieces move forward by moving to lower numbered rows. The following image shows four possible simple moves:

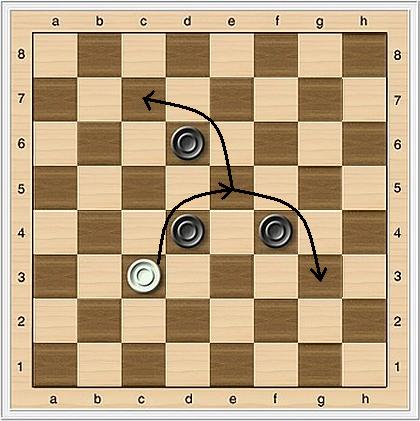
A capturing move for a "man" consists of jumping over a diagonally adjacent opponent piece (this piece is considered to be captured) and landing in the empty square immediately beyond that piece. After landing, if another capture is possible from that new square, it must be performed as part of the same turn. This can happen multiple times within the same turn. If multiple captures are possible from a position, any one of them can be performed. When capturing, pieces can move in any of the four diagonal directions, and can change directions after each landing. After the end of a capturing move all captured pieces are removed from the board. It is not allowed to capture the same opponent piece more than once during the same turn. The image below shows two possible capturing moves - c3 to e5 to c7, and c3 to e5 to g3. Note that, for example, the capturing move c3 to e5 to g3 to e5 to c7 is not valid because it requires jumping two times over the piece at f4.
When a "man" reaches the far side of the board (row 8 for white pieces, and row 1 for black pieces), it is promoted to a "king". A "king" moves differently than a "man". A simple move for a "king" consists of moving one or more squares in any of the four diagonal directions. All the squares in the path, including the ending square, must be empty.
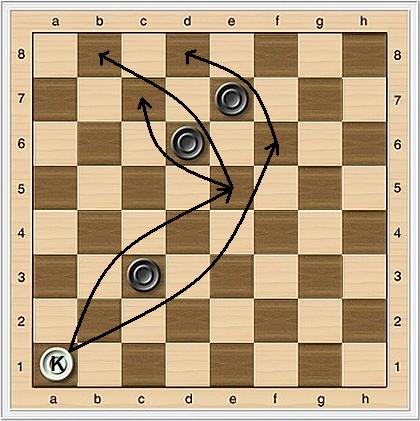
A capturing move for a "king" consists of moving zero or more squares diagonally, jumping over an opponent piece, and then moving zero or more additional squares along the same path. With the exception of the square containing the jumped opponent piece, all squares in the path must be empty, and the path must form a straight diagonal line. When the "king" moves zero or more additional squares after jumping over the opponent, it must stop at a square from which it can perform another capture if possible. If there are multiple such squares, any one of them can be chosen. If there are no such squares, it can stop at any empty square. The "king" must continue making captures within the same turn as long as possible captures exist. As with "men", all captured pieces are removed from the board after the end of move, and it is not allowed to capture the same opponent piece more than once during the same turn. The following image shows the three possible moves a white king can make in a single turn - a1 to e5 to c7, a1 to e5 to b8, and a1 to f6 to d8:
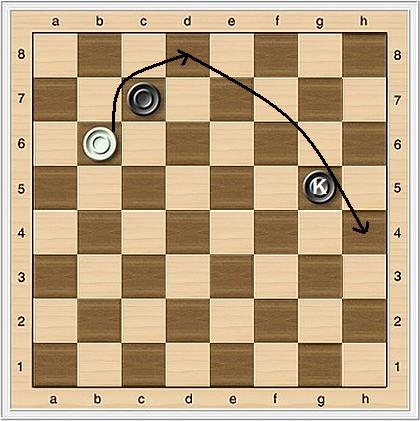
If a "man" reaches the far side of the board as the result of a capturing move, it becomes a "king" and must continue capturing if possible, but as a "king". The following image shows a white "man" jumping a black piece, becoming a "king", and continuing to capture as a "king":
Your task is to write the first part of an AI engine. Given the current configuration of the board, and the player with the current turn, you must determine all the possible moves for that player. The board will be given in the String[] board, the first element of which describes row 8 from left to right, the second element of which describes row 7 from left to right, etc. '.' characters denote empty cells, 'b' and 'w' denote black and white "men", respectively, and 'B' and 'W' denote black and white "kings", respectively. The current player is given in the String turn, and will be either "BLACK" or "WHITE" (quotes for clarity). Return a String[] containing all the possible moves for the current player in lexicographical order. Each move is described by the sequence of cells in which the piece lands, starting with the piece's original position. In a simple move, cells are separated by '-' characters, and in a capturing move, cells are separated by ':' characters. See examples for further clarification.
|