Problem Statement |
| |
You are given several rectangles in the Cartesian plane with sides parallel to the axes. They are
represented by the int[]s x1, y1, x2 and y2, where
(x1[i], y1[i]) are the coordinates of the lower-left corner and (x2[i], y2[i])
are the coordinates of the upper-right corner of the i-th rectangle.
Your task is to color exactly K rectangles in such a way that the visible colored area is as large as
possible. If some area is covered by more than one rectangle, only the part of the rectangle with the
highest index is visible (see example 0). Return a int[] containing exactly K
elements - the 0-based indices of the colored rectangles. If there are several possible return values,
return the one that comes earliest lexicographically. A int[] a1 comes before a int[]
a2 lexicographically if a1 has a smaller element at the first index where they differ.
|
| |
Definition |
| | | Class: | ColoringRectangles | | Method: | maxColoredArea | | Parameters: | int[], int[], int[], int[], int | | Returns: | int[] | | Method signature: | int[] maxColoredArea(int[] x1, int[] y1, int[] x2, int[] y2, int K) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | x1 will contain between 1 and 50 elements, inclusive. |
| - | x1, y1, x2 and y2 will all contain same number of elements. |
| - | Each element of x1, x2, y1 and y2 will be between -10000 and 10000, inclusive. |
| - | x1[i] will be strictly less than x2[i] for all i. |
| - | y1[i] will be strictly less than y2[i] for all i. |
| - | K will be between 1 and number of elements in x1, inclusive. |
| |
Examples |
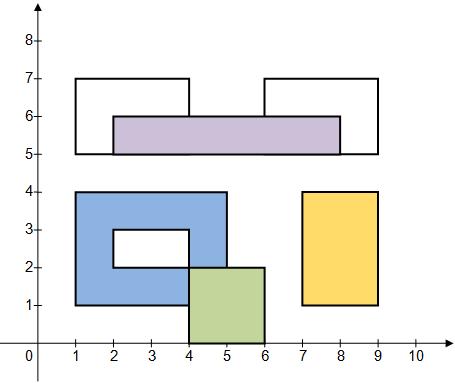
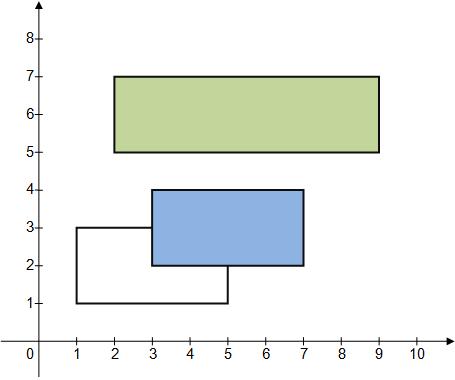
| 0) | |
| | {1, 3, 2} | {1, 2, 5} | {5, 7, 9} | {3, 4, 7} | 2 |
| Returns: {1, 2 } | If you color rectangles with indices 0 and 1, the visible colored area will be 6 + 8 = 14.
If you color rectangles with indices 0 and 2, the visible colored area will be 6 + 14 = 20.
If you color rectangles with indices 1 and 2, the visible colored area will be 8 + 14 = 22.
 |
|
|
| 1) | |
| | {1, 2, 4, 7, 1, 6, 2} | {1, 2, 0, 1, 5, 5, 5} | {5, 4, 6, 9, 4, 9, 8} | {4, 3, 2, 4, 7, 7, 6} | 4 |
| Returns: {0, 2, 3, 6 } | |
|
| 2) | |
| | {-5646, -5814, -1459, 6522, -6564, 1450, -2132, 6911, -9062} | {1463, 2872, -5496, 5163, -8549, -7835, 4725, 2420, 6350} | {471, -626, -1110, 7374, 5856, 3365, 1934, 7775, 3495} | {5776, 4869, 7008, 8802, -1730, -7161, 8571, 8905, 7573} | 2 |
| Returns: {4, 8 } | |
|
| 3) | |
| | {-3591, 1138, -4086, -9022, 4306, -5936, 8559, -6010, 9427, 3327, -4508, 6444, -4004,
-3183, -7990, -1338, -4241, -5417, 1057, -8444, -9621, 4001, -4373, -6506, -1068, -5504} | {347, -1456, 117, -5894, -9053, -762, 6132, -9380, 3501, -8102, -2173, -271, -6271,
-7546, -4792, -4591, -9430, 1185, -914, -5802, -1424, -9786, -3138, 1433, -9060, 2509} | {7239, 4410, 7929, -2195, 6088, 8953, 8700, -1599, 9886, 8966, -3672, 7583, -1242,
1923, 9511, 3815, -3549, 7758, 1323, 1730, -1868, 5412, 727, 8930, 6211, -4513} | {6643, 7598, 4989, 3169, 1833, 4242, 8541, 8428, 5596, -2838, 2957, 1326, -5883,
1850, 7082, 9761, -6129, 4223, 8920, -5237, 992, -5976, 2830, 4338, -8927, 6236} | 15 |
| Returns: {3, 7, 9, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25 } | |
|
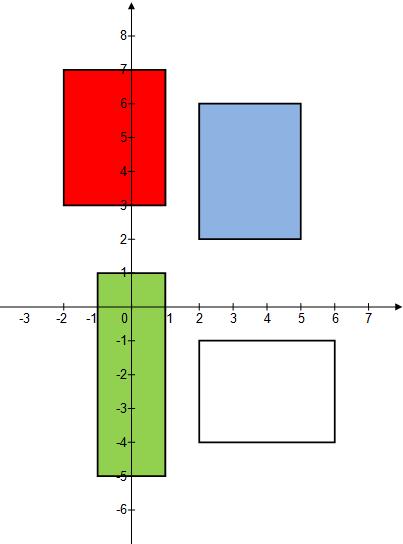
| 4) | |
| | {-1, 2, -2, 2} | {-5, 2, 3, -4} | {1, 5, 1, 6} | {1, 6, 7, -1} | 3 |
| Returns: {0, 1, 2 } | All rectangles are of equal size and no two of them are overlapping.
 |
|
|