TopCoder problem "CactusCount" used in SRM 419 (Division II Level Three)

Problem Statement

A vertex cactus is a connected undirected graph such that each vertex belongs to at most one simple cycle. A simple cycle is a cycle that doesn't pass through any vertex more than once. For example, the graph pictured below is a vertex cactus:

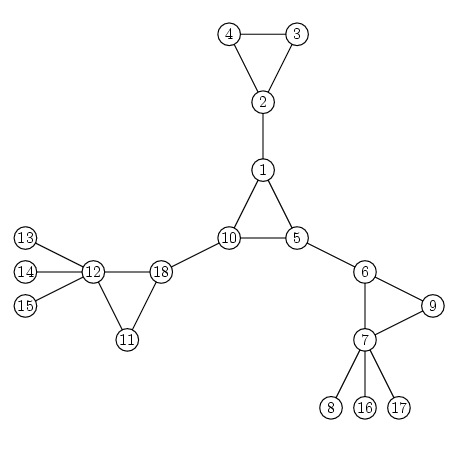
You are given an int n, the number of vertices in a graph G. The vertices are numbered from 1 to n. The edges in G are given in the String[] edges. Concatenate the elements of edges to get a comma-separated list of integer pairs. The integers in each pair are separated by a space. The pair "i j" (quotes for clarity) means that there is an edge between vertices i and j. Return the number of connected components of G that are vertex cacti.

Definition

Class:	CactusCount
Method:	countCacti
Parameters:	int, String[]
Returns:	int
Method signature:	int countCacti(int n, String[] edges)
(be sure your method is public)

Notes

A connected component of a graph G is a set of vertices such that each pair of vertices in the set is connected by a path, and no vertex outside the set is connected to any vertex within the set.

Constraints

n will be between 1 and 200, inclusive.

edges will contain between 0 and 50 elements, inclusive.

Each element of edges will contain between 1 and 50 characters, inclusive.

When concatenated, edges will contain a comma separated list of integer pairs.

The integers within each pair will be separated by a space.

The integers within each pair will be distinct.

Each integer will be between 1 and n, inclusive, with no leading zeroes.

Every pair of vertices will be connected by at most one edge.

Examples

{"1 2,1 3,2 3"}

Returns: 1

One cycle is a vertex cactus.

{}

Returns: 10

Here each vertex is a component by itself. A graph with one vertex is a vertex cactus.

{"1 2,3 4,4 5"}

Returns: 2

Both components are trees. A tree is a vertex cactus.

{"1 2,2 3,3 4,4 5,5 3,1 3,6 7,7 8,6 8,8 9,9 1",
 "0,10 11,11 9,12 13,14 15,15 16,16 17,14 17,14 16"}

Returns: 2

Here are two cacti and two non-cacti. The component with vertices 1, 2, 3, 4 and 5 is not a vertex cactus because vertex 3 belongs to two cycles: 1-2-3 and 3-4-5. The component with vertices 14, 15, 16 and 17 is not a vertex cactus either. Vertex 14, for example, belongs to more than one cycle.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10077

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13510&pm=10077

Writer:

andrewzta

Testers:

PabloGilberto , Olexiy , marek.cygan , ivan_metelsky

Problem categories:

Graph Theory, String Parsing