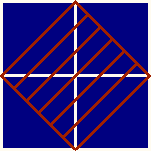
TopCoder problem "SettingTents" used in SRM 433 (Division I Level Two)



Problem Statement

    

Once upon a time, there lived a migrant barbarian tribe. Every time it settled down, a tent was set for the chief of the tribe. First, an area was selected and divided into NxM squares with side lengths of 1 unit. Then, they chose a site for the tent in such a way that every vertex of its base coincided with some vertex of one of the squares. According to an ancient tradition, the base had to be a rhomb. For example, there are all 6 different possible sites for the tent in a 2x2 area:



       



       


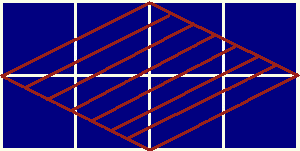
An example of a tent in a 4x2 area:
   


For a given N and M, return the number of different possible sites for the chief's tent. Two sites are different if there is at least one vertex which belongs to one site but not the other.

 

Definition

    
Class:SettingTents
Method:countSites
Parameters:int, int
Returns:int
Method signature:int countSites(int N, int M)
(be sure your method is public)
    
 

Notes

-A rhomb is a four-sided polygon with sides of equal length.
-The tent must have non-zero area.
 

Constraints

-N will be between 1 and 100, inclusive.
-M will be between 1 and 100, inclusive.
 

Examples

0)
    
2
2
Returns: 6
The example from the problem statement.
1)
    
1
6
Returns: 6
The only possible sites are the squares of the area themselves.
2)
    
6
8
Returns: 527

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10191

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13695&pm=10191

Writer:

gojira_tc

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem categories:

Geometry, Simple Search, Iteration