TopCoder problem "CellRemoval" used in SRM 435 (Division I Level One , Division II Level Two)



Problem Statement

    In biology, organisms have the following property: Starting from the first cell (the zygote), each cell during an organism's development process either divides into 2 other cells or does not divide at all. An organism is mature when all of its cells will not divide any further.



Let's assign a unique number to each cell in an organism's development process. For example, consider a species in which each organism starts with cell 0, which divides into cells 1 and 2. Cell 1 divides into cells 3 and 4. Cells 2, 3 and 4 do not divide. Every mature organism of this species will consist of exactly 3 cells - 2, 3 and 4.



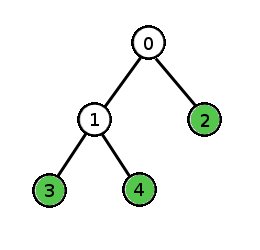
During the development process, if we kill a cell, it will be absent in the mature form of the organism. If that cell happens to be a cell that divides, then the mature organism will be missing all of the cell's descendants as well because the cell is killed before it has a chance to divide. For example, in the organism described above, if we kill cell 1 during the development process, the mature organism will contain only cell 2.



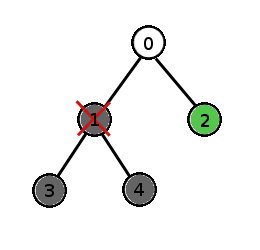
You are given a int[] parentCell describing the development process of an organism. The i-th element of parentCell is the parent cell of cell i (where i is a 0-based index). The zygote's parent is -1. Return the number of cells the mature form of this organism would have if you killed cell deletedCell during the development process.
 

Definition

    
Class:CellRemoval
Method:cellsLeft
Parameters:int[], int
Returns:int
Method signature:int cellsLeft(int[] parent, int deletedCell)
(be sure your method is public)
    
 

Constraints

-parentCell will contain exactly N elements, where N is an odd integer between 1 and 50, inclusive.
-There will be exactly one "-1" element in parentCell.
-Every element of parentCell will be between -1 and N-1, inclusive.
-parentCell will form a binary tree.
-deletedCell will be between 0 and N-1, inclusive.
 

Examples

0)
    
{-1,0,0,1,1}
2
Returns: 2
This is the example organism from the problem statement. If we kill cell 2, there will still be two cells left (3 and 4).
1)
    
{-1,0,0,1,1}
1
Returns: 1
This is the example organism from the problem statement. If we kill cell 1, the only cell left will be cell 2. Cells 3 and 4 will not exist because cell 1 is their ancestor.
2)
    
{-1,0,0,1,1}
0
Returns: 0
If we kill the zygote, there is nothing left.
3)
    
{-1,0,0,2,2,4,4,6,6}
4
Returns: 2
4)
    
{26,2,32,36,40,19,43,24,30,13,21,14,24,21,19,4,30,10,44,12,7,32,17,43,
 35,18,7,36,10,16,5,38,35,4,13,-1,16,26,1,12,2,5,18,40,1,17,38,44,14}
24
Returns: 14

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10275

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13697&pm=10275

Writer:

almelv

Testers:

PabloGilberto , Olexiy , ivan_metelsky

Problem categories:

Graph Theory, Simple Search, Iteration