Problem Statement |
| | Circles Country is a country that contains several circular-shaped districts. Some districts may be situated inside other districts, but their borders do not intersect or touch. Qatam is a resident of Circles Country. When he travels between two locations, he always tries to cross the fewest number of district borders as possible because crossing borders is usually a laborious task.
Imagine Circles Country as an infinite plane. You are given int[]s X, Y and R, where (X[i], Y[i]) are the coordinates of the i-th district's center and R[i] is its radius. Qatam is currently at point (x1,y1) and he needs to get to point (x2,y2). Neither of these points lies on a district border. Return the minimal number of district borders he must cross to get to his destination.
|
| |
Definition |
| | | Class: | CirclesCountry | | Method: | leastBorders | | Parameters: | int[], int[], int[], int, int, int, int | | Returns: | int | | Method signature: | int leastBorders(int[] X, int[] Y, int[] R, int x1, int y1, int x2, int y2) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | X will contain between 1 and 50 elements, inclusive. |
| - | X, Y and R will each contain the same number of elements. |
| - | Each element of X and Y will be between -1000 and 1000, inclusive. |
| - | Each element of R will be between 1 and 1000, inclusive. |
| - | x1, y1, x2 and y2 will be between -1000 and 1000, inclusive. |
| - | No two circumferences will have common points. |
| - | The points (x1,y1) and (x2,y2) will not lie on any of the circumferences. |
| |
Examples |
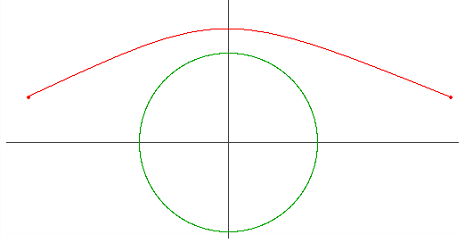
| 0) | |
| | |
| 1) | |
| | {0,-6,6} | {0,1,2} | {2,2,2} | -5 | 1 | 5 | 1 |
| Returns: 2 | |
|
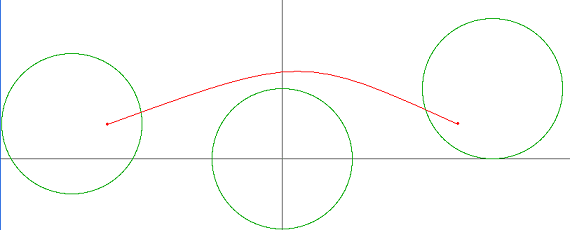
| 2) | |
| | {1,-3,2,5,-4,12,12} | {1,-1,2,5,5,1,1} | {8,1,2,1,1,1,2} | -5 | 1 | 12 | 1 |
| Returns: 3 | |
|
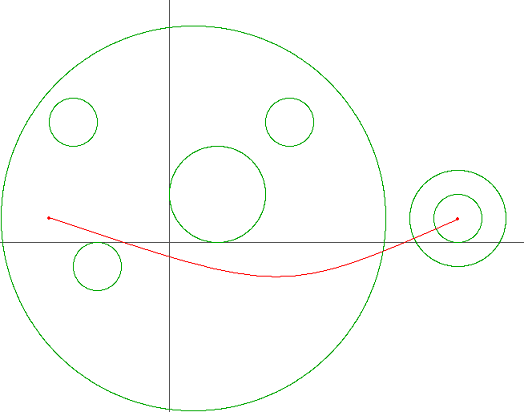
| 3) | |
| | {-3,2,2,0,-4,12,12,12} | {-1,2,3,1,5,1,1,1} | {1,3,1,7,1,1,2,3} | 2 | 3 | 13 | 2 |
| Returns: 5 | |
|
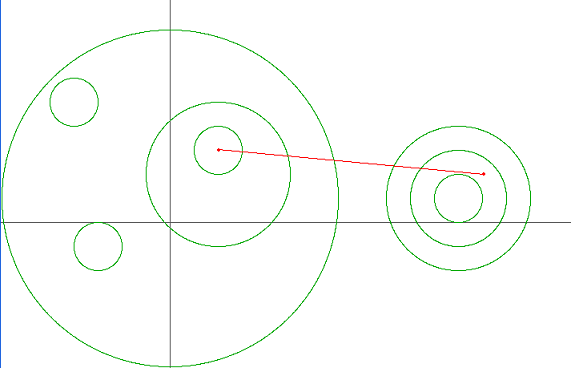
| 4) | |
| | {-107,-38,140,148,-198,172,-179,148,176,153,-56,-187} | {175,-115,23,-2,-49,-151,-52,42,0,68,109,-174} | {135,42,70,39,89,39,43,150,10,120,16,8} | 102 | 16 | 19 | -108 |
| Returns: 3 | |
|