Problem Statement |
| | A team of geologists is searching a site expected to have a rich mineral deposit. Both the site and the deposit can be represented by convex polygons such that the deposit polygon is located completely inside the site polygon. The coordinates of the site polygon's vertices will be given in the int[]s siteX and siteY, and the coordinates of the deposit polygon's vertices will be given in the int[]s depositX and depositY. Each of these two sets of points is given in counter-clockwise order, starting from an arbitrary initial vertex. The size of the team is very small compared to the sizes of the site and deposit, so we shall represent the team by a point.
Since the site is so large, the team cannot explore all of it. Instead, they will start at a point chosen uniformly at random from all points on the site boundary, and move in a straight line towards a point on the site boundary which is farthest away from the starting point. If several points on the boundary are farthest away from the starting point, the team chooses one of them with equal probability. The team's analysts are hoping that this method will give the team a high chance of finding the deposit.
Let us say that the team finds the deposit if the team's path and the deposit region intersect in at least one point. Return the probability that the team finds the deposit. |
| |
Definition |
| | | Class: | Deposit | | Method: | successProbability | | Parameters: | int[], int[], int[], int[] | | Returns: | double | | Method signature: | double successProbability(int[] siteX, int[] siteY, int[] depositX, int[] depositY) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | The returned value must have an absolute or relative error less than 1e-9. |
| - | A polygon is convex if it does not intersect itself, and every straight line joining any two interior points of the polygon is entirely contained in the polygon's interior. |
| |
Constraints |
| - | siteX, siteY, depositX and depositY will each contain between 3 and 50 elements, inclusive. |
| - | siteX and siteY will contain the same number of elements. |
| - | depositX and depositY will contain the same number of elements. |
| - | Each element of siteX, siteY, depositX and depositY will be between -1000 and 1000, inclusive. |
| - | The points (siteX[i], siteY[i]), taken in order, will describe a counterclockwise traversal of vertices in a convex polygon. |
| - | The points (depositX[i], depositY[i]), taken in order, will describe a counterclockwise traversal of vertices in a convex polygon. |
| - | In each of the polygons, no three adjacent vertices will lie on the same line. |
| - | The deposit polygon will be located entirely in the interior of the site polygon. The boundaries of the two polygons will not intersect. |
| |
Examples |
| 0) | |
| | {0,4,4,0} | {0,0,4,4} | {1,2,2,1} | {1,1,2,2} |
| Returns: 0.6666666666666666 | In the picture below, the outer square represents the site and the inner square represents the deposit. The blue sections of the site's perimeter consist of points which would lead to failure if they were chosen as the start of the team's path. The coordinates of these ranges are given (in blue). The white sections show the starting points for a successful path.
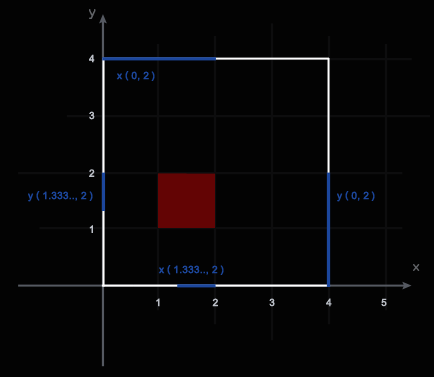
|
|
|
| 1) | |
| | {0,4,4,0} | {0,0,4,4} | {1,3,3,1} | {1,1,3,3} |
| Returns: 1.0 | Here, the team will always find the deposit.
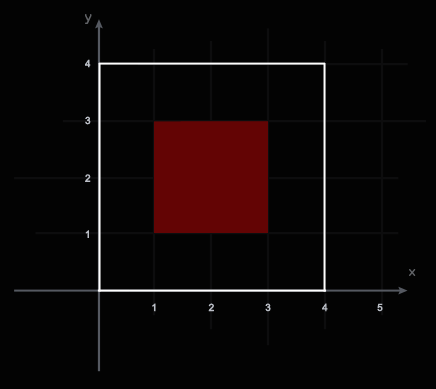
|
|
|
| 2) | |
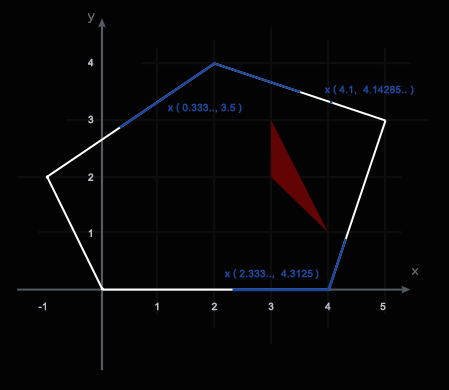
| | {5,2,-1,0,4} | {3,4,2,0,0} | {3,3,4} | {3,2,1} |
| Returns: 0.6112700209855423 | |
|
| 3) | |
| | {200,-99,-405,-601,-708,-494,-300,-88} | {520,516,407,321,104,-97,-221,-101} | {-101,-201,-296,-400,-402} | {318,396,402,305,200} |
| Returns: 0.49892756207100747 | |
|
| 4) | |
| | {-3,6,10,10,-2} | {-1,-10,-9,7,3} | {3,5,6,4} | {-5,-7,-6,-4} |
| Returns: 0.16641662251521538 | |
|
| 5) | |
| | {-2,4,-2}
| {-2,-2,8}
| {-1,0,0}
| {0,-1,0}
|
| Returns: 0.04518850219072291 | |
|