TopCoder problem "PlanarGraphShop" used in SRM 453.5 (Division I Level Two)



Problem Statement

    

In the Kocurkovo village there is a shop that sells simple planar graphs. (See Notes for a definition.)

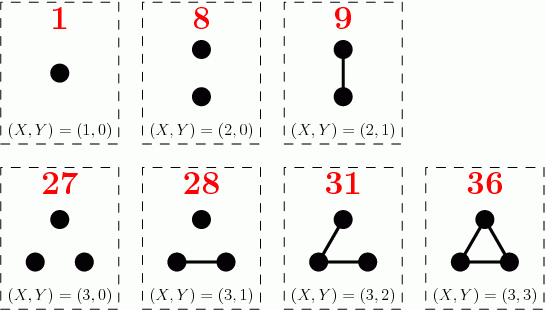
The cost of any graph with X vertices and Y edges is (X^3 + Y^2) gold coins.

Monika has N gold coins, and she wants to spend all of them on simple planar graphs.

Write a method that gets the value N and computes the minimum number of simple planar graphs Monika has to buy in order to spend exactly N gold coins. She is allowed to buy multiple graphs of the same type.

 

Definition

    
Class:PlanarGraphShop
Method:bestCount
Parameters:int
Returns:int
Method signature:int bestCount(int N)
(be sure your method is public)
    
 

Notes

-A simple graph is an ordered pair (V,E) where V is a finite non-empty set of objects called vertices, and E is a finite set of edges. Each edge is a two-element subset of V.

(You can find drawings of several graphs in Example #3.)
-Note that a simple graph does not contain any loops (edges that connect a vertex to itself) and any duplicate edges. In other words, each edge connects two different vertices, and each pair of vertices is connected by at most one edge.
-A graph is called planar if it has a drawing in the plane such that no two edges intersect.
-Note that a simple planar graph does not have to be connected.
 

Constraints

-N will be between 1 and 50,000, inclusive.
 

Examples

0)
    
36
Returns: 1
For 36 gold coins she can buy a triangle: a simple planar graph with 3 vertices and 3 edges.
1)
    
7
Returns: 7
The only simple planar graph that costs 7 gold coins or less is the graph that consists of a single vertex (and no edges). This graph costs 1^3 + 0^2 = 1, so Monika has to buy 7 of them.
2)
    
72
Returns: 2
She can buy 2 triangles for 36 gold coins each. No simple planar graph costs exactly 72 gold coins, hence the optimal answer in this case is 2.
3)
    
46
Returns: 3

All the graphs Monika can afford are shown in the following picture:

One optimal solution is to buy graphs worth 1 + 9 + 36 gold coins.

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10412

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=14174&pm=10412

Writer:

misof

Testers:

PabloGilberto , Yarin , ivan_metelsky

Problem categories:

Dynamic Programming, Graph Theory