Problem Statement |
| | Onise likes to play with paper and paint. He has a piece of paper with dimensions width x height. He does the following steps with the paper:
- Fold the paper along the line x = xfold (the left side of the paper is folded over the right side).
- Divide the paper vertically into cnt+1 equal sections. Then, cnt times, take the topmost section and fold it over the section below it.
- Paint a rectangle with the lower-left corner at (x1, y1) and the upper-right corner at (x2, y2). Note that (0, 0) is now the lower-left corner of the paper in its current folded state, not its original state. The paint will seep through all the layers of the folded paper. See the image below for clarification.
- Unfold the paper.
For example, let's say Onise has a piece of paper that is 5 x 6. He performs the described steps where xfold is 2, cnt is 2, and the coordinates of the painted rectangle's corners are (1, 1) and (3, 2). The following will happen (note that the paper starts out blue in the images and gets painted white):
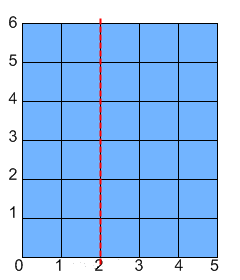
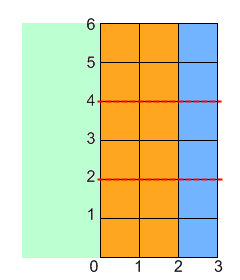
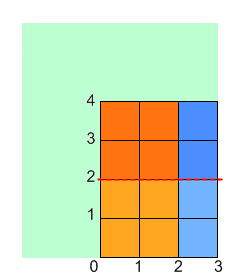
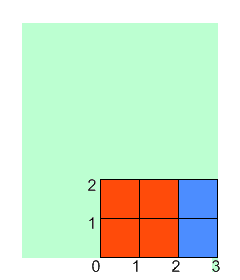
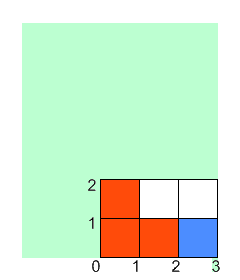
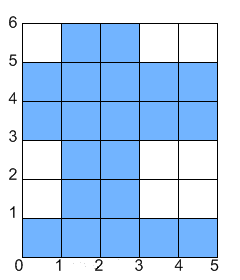
You are given ints width and height, and ints xfold, cnt, x1, y1, x2 and y2. Return the total area of of the paper that is not covered in paint after Onise is done. |
| |
Definition |
| | | Class: | PaperAndPaintEasy | | Method: | computeArea | | Parameters: | int, int, int, int, int, int, int, int | | Returns: | long | | Method signature: | long computeArea(int width, int height, int xfold, int cnt, int x1, int y1, int x2, int y2) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | width and height will be between 1 and 10^9, inclusive. |
| - | xfold will be between 0 and width, inclusive. |
| - | cnt will be between 0 and 1000, inclusive. |
| - | cnt+1 will be a divisor of height. |
| - | 0 <= x1 < x2 <= max(xfold, width-xfold) and 0 <= y1 < y2 <= height/(cnt+1). |
| |
Examples |
| 0) | |
| | | Returns: 21 | | The example from the problem statement. |
|
|
| 1) | |
| | |
| 2) | |
| | |
| 3) | |
| | |
| 4) | |
| | |
| 5) | |
| | |





