Problem Statement |
| | NOTE: This problem statement contains images that may not display properly if viewed outside of the applet.
Alice loves mazes so much that she spends most of her spare time drawing new mazes on sheets of graph paper. These mazes work as follows. Every cell is either an empty space or a wall. One of the empty cells is the starting cell and one of the other empty cells is the ending cell. To solve the maze, you must draw a path from the starting cell to the ending cell without lifting your pen. From each cell, you are only allowed to move to an empty neighboring cell. Two cells are neighbors if they share a common side.
Alice is so obsessed that she forces her friend Bob to solve her mazes over and over again. Lately, she began cheating by making her mazes unsolvable. However, Bob, being an avid cheater himself, discovered that he could solve those mazes by folding the sheet of paper until the maze became solvable. Alice did not initially like the fact that Bob had thwarted her attempts to make unsolvable mazes, but she eventually figured out that drawing mazes that can only be solved by folding the paper would be far more interesting than drawing unsolvable mazes.
Alice came up with a new method of creating mazes and a new set of rules. She now draws on both sides of the graph paper. The starting cell is always on the front, but the ending cell may be on either side. Bob must put the sheet of paper on a table with the front side facing up. On each move, he must do one of the following:
- Move to an empty neighboring cell. The rules here are the same as before. He can only move to cells that are currently visible.
- Fold the paper once. This is only allowed if the paper is not already in a folded state. The folding line must coincide with a vertical line on the graph paper's grid. The fold must not cover the cell in which Bob is currently located. Horizontal, diagonal or any fold operation with a folding line that does not coincide with a vertical grid line are considered illegal.
- Unfold the paper if it's currently folded. This will return the paper to its initial state. This is only allowed if doing so will not remove the current cell from view.
For example, consider the following case in which we can see both sides of the sheet (the back side depicted is the part of the sheet that would be visible after rotating it 180 degrees about the vertical axis):
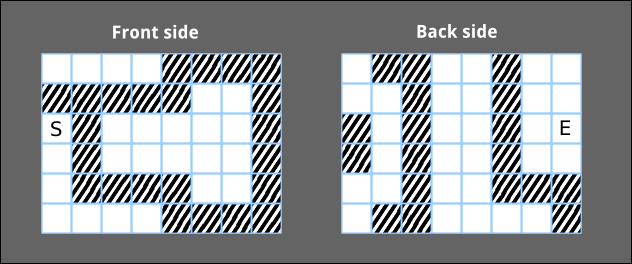
In this case, the third vertical line from the left is used as a folding line.
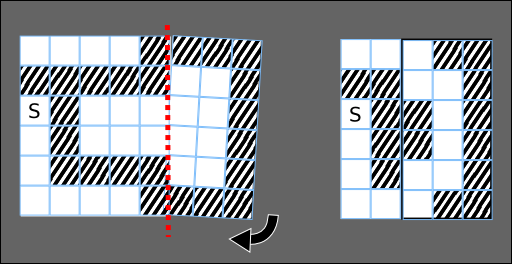
After folding the paper, it is now possible to move from the starting cell to the second cell from the left in the top row. After that, the paper is unfolded.
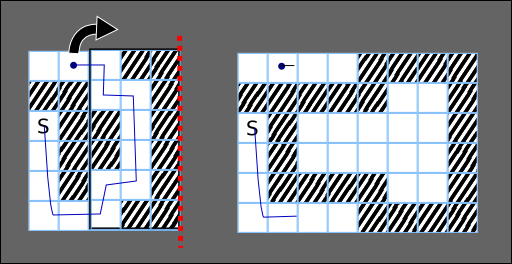
Then, move one cell to the right and perform another fold.
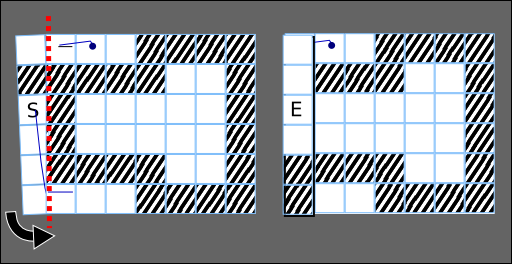
Notice that you can fold up either the right or left side of the paper as long as you follow all the rules. After the second fold, the ending cell becomes visible, and it is now possible to move there.
Your task is to help Bob cheat by determining the fastest way to solve these mazes. You are given String[]s frontSide and backSide, describing the front and back sides of the paper, respectively. The j-th character of the i-th element of each String[] represents the cell at row i, column j. Empty cells are denoted by '.', walls are denoted by '#', the starting cell is denoted by 'S' and the ending cell is denoted by 'E'. backSide describes what you would see if you flipped the paper over by rotating it 180 degrees about the vertical axis. Return the minimum number of steps required to solve the maze. If it is not possible to solve the maze, return -1 instead. |
| |
Definition |
| | | Class: | FoldingMaze | | Method: | solve | | Parameters: | String[], String[] | | Returns: | int | | Method signature: | int solve(String[] frontSide, String[] backSide) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | frontSide and backSide will contain an equal number of elements h, where h is between 2 and 50, inclusive. |
| - | Each element of frontSide and backSide will contain an equal number of characters w, where w is between 2 and 50, inclusive. |
| - | Each element of frontSide and backSide will contain only '#', '.', 'S' or 'E' as characters. |
| - | Exactly one character in frontSide will be 'S'. |
| - | backSide will not contain any 'S' characters. |
| - | The total number of 'E' characters in frontSide and backSide will be exactly 1. |
| |
Examples |
| 0) | |
| | {"...E",
"....",
"S..."} | {"####",
"####",
"####"} |
| Returns: 5 | | The back of the sheet is full of walls. Therefore, it is not advantageous to fold the sheet at all. |
|
|
| 1) | |
| | {"...E",
"###.",
"S.#."} | {"....",
"....",
"...."} |
| Returns: 9 | We can first fold the right side like this:
...
##.
S..
Then we get to row 0, column 1:
.*.
##.
...
We may now unfold the maze:
.*.E
###.
..#.
Nine steps are required in total. |
|
|
| 2) | |
| | {"....",
"S.#.",
"...."} | {"#...",
"##.E",
".#.#"} |
| Returns: 6 | This time the exit is on the back of the sheet.
1) Go to row 0, column 2:
..*.
..#.
....
2) Fold the left side of the sheet:
.*.
E#.
#..
3) Go to the exit.
|
|
|
| 3) | |
| | {"....####",
"#####..#",
"S#.....#",
".#.....#",
".####..#",
"....####"} | {".##..#..",
"..#..#..",
"#.#..#.E",
"#.#..#..",
"..#..###",
".##....#"} |
| Returns: 20 | | The solution for this case was detailed in the statement. |
|
|
| 4) | |
| | {"....####",
"#####..#",
"S#.....#",
".#.....#",
".####..#",
"....####"} | {".#####.#",
"..####..",
"#.####.E",
"#.####..",
"..######",
"........"} |
| Returns: -1 | | Note that you are not allowed to fold the paper along horizontal lines. |
|
|



