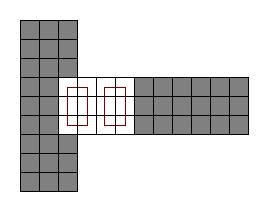
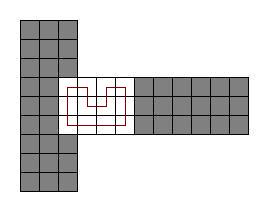
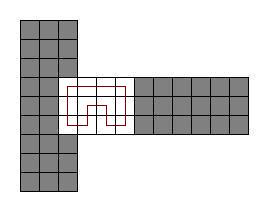
You are given a 3x3x3 cube. Each face of the cube contains a 3x3 grid of nine squares. Some of the squares are painted and the rest are unpainted. Your task is to calculate the number of ways you can cover all the unpainted squares with "cube-cycles".
A cube-cycle is a sequence of 3 or more squares, where each square is "cube-adjacent" to the next square, and the last square is "cube-adjacent" to the first square. All squares in a cube-cycle must be distinct. Two squares are cube-adjacent if they share a common edge. That common edge can be on a face or on an edge of the cube. Each square in the cube has exactly four cube-adjacent squares.
Note that two cube-cycles might be distinct even if they contain the same set of squares. See example 0.
You are given the cube as a String[] containing 54 characters, where each character represents a single square. The String[] will be formatted as a net of the cube, as shown below:
+---+
| |
+---+---+---+---+
| | | | |
+---+---+---+---+
| |
+---+
Painted squares are represented by '*' characters and unpainted squares are represented by '.' characters. You are only allowed to cover unpainted squares with cube-cycles. You are not allowed to cover painted squares. All unpainted squares must be covered, and no two cube-cycles can overlap each other. Return the number of ways you can cover the cube modulo 1,000,000,007.
|