TopCoder problem "MountainRoad" used in SRM 449 (Division II Level One)



Problem Statement

    

Your friend is going to the mountains on vacation. He will climb up and down several mountains, and he has asked you to calculate his total walking distance.



To simplify this task, everything will be represented on a 2-dimensional cartesian plane. The ground is represented as the x-axis, and the mountains are represented as the union of several isosceles triangles. You are given int[]s start and finish. For each index i, construct an isosceles right triangle with its hypotenuse lying on the ground from point start[i] to point finish[i].

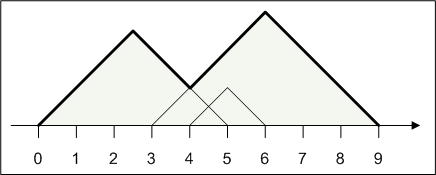
The mountains are guaranteed to form a single connected non-degenerate polygon, where the height is positive everywhere between the start and end points. The path your friend will walk is defined as the upper part of this mountain, shown in bold in the figure above. Return the length of this path.



 

Definition

    
Class:MountainRoad
Method:findDistance
Parameters:int[], int[]
Returns:double
Method signature:double findDistance(int[] start, int[] finish)
(be sure your method is public)
    
 

Notes

-The returned value must be accurate to within a relative or absolute value of 1E-9.
-An isosceles right triangle is a triangle with angles 90, 45 and 45 degrees. The hypotenuse of such a triangle is the side opposite the 90 degree angle.
 

Constraints

-start will contain between 1 and 50 elements, inclusive.
-start and finish will contain the same number of elements.
-Each element of start and finish will be between -1000 and 1000, inclusive.
-For every i start[i] will be strictly less than finish[i].
-The union of the isosceles triangles described in start and finish will be a single connected nondegenerate polygon.
 

Examples

0)
    
{1}
{7}
Returns: 8.485281374238571
In this case there is only one mountain.
1)
    
{0,3,4}
{5,9,6}
Returns: 12.727922061357857
This situation with three mountains is shown in the figure above.
2)
    
{1,4,5,6,-10}
{101,102,101,100,99}
Returns: 158.39191898578665
3)
    
{-5,-3}
{-2,-2}
Returns: 4.242640687119286

Problem url:

http://www.topcoder.com/stat?c=problem_statement&pm=10546

Problem stats url:

http://www.topcoder.com/tc?module=ProblemDetail&rd=13903&pm=10546

Writer:

dzhulgakov

Testers:

PabloGilberto , ivan_metelsky , zhuzeyuan

Problem categories:

Simple Math, Simple Search, Iteration