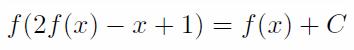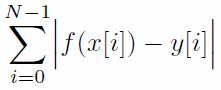Problem Statement |
| | f is a function from integers to integers. In other words, f is defined over integers, and f(x) is an integer for all integers x. You are given an integer C. f is called C-beautiful if the following equality is satisfied for all integers x:
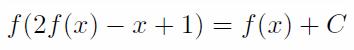
Return the minimal possible value of the following formula when f is C-beautiful:
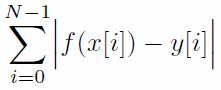
Use the following recursive definitions to generate the sequences x and y:
- x[0] = xzero
- For all integer i between 1 and N-1, inclusive, x[i] = (x[i-1] * xprod + xadd) % xmod
- y[0] = yzero
- For all integer i between 1 and N-1, inclusive, y[i] = (y[i-1] * yprod + yadd) % ymod
|
| |
Definition |
| | | Class: | FunctionalEquation | | Method: | minAbsSum | | Parameters: | int, int, int, int, int, int, int, int, int, int | | Returns: | long | | Method signature: | long minAbsSum(int C, int N, int xzero, int xprod, int xadd, int xmod, int yzero, int yprod, int yadd, int ymod) | | (be sure your method is public) |
|
| |
|
| |
Notes |
| - | 64-bit integers should be used to generate the sequences x and y to avoid overflow. |
| |
Constraints |
| - | C will be between 1 and 16, inclusive. |
| - | N will be between 1 and 10,000, inclusive. |
| - | xmod and ymod will each be between 1 and 1,000,000,000, inclusive. |
| - | xzero, xprod and xadd will each be between 0 and xmod - 1, inclusive. |
| - | yzero, yprod and yadd will each be between 0 and ymod - 1, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 0 | f(x) = x + 1 is a 3-beautiful function.
Since x = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} and y = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10},
the sum of |f(x[i]) - y[i]| is 0. |
|
|
| 1) | |
| | | Returns: 5 | | x and y are the same as in example 0, but f(x) = x + 1 is not a 4-beautiful function. |
|
|
| 2) | |
| | 16 | 10000 | 654816386 | 163457813 | 165911619 | 987654321 | 817645381 | 871564816 | 614735118 | 876543210 |
| Returns: 3150803357206 | |
|