Problem Statement |
| | Suppose that there are N numbers written in a row. A row above this one consists of N-1 numbers, the i-th of which is the sum of the i-th and (i+1)-th elements of the first row. Every next row contains one number less than the previous one and every element is the sum of the two corresponding elements in the row below. The N-th row contains a single number. For example, if the initial numbers are {2,1,2,4}, the whole structure will look like this:
15
6 9
3 3 6
2 1 2 4
We shall refer to such a structure as a number pyramid. Two number pyramids are equal if all the numbers at corresponding positions are equal.
Given ints baseLength and top, compute the total number of different number pyramids consisting of positive integers, having baseLength elements in the first row and the value at the top equal to top. Since the number of such pyramids might be enormous, return the result modulo 1,000,000,009. |
| |
Definition |
| | | Class: | NumberPyramids | | Method: | count | | Parameters: | int, int | | Returns: | int | | Method signature: | int count(int baseLength, int top) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | baseLength will be between 2 and 1,000,000, inclusive. |
| - | top will be between 1 and 1,000,000, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 2 | The following are two possible pyramids with 3 numbers in the base and the number 5 at the top:
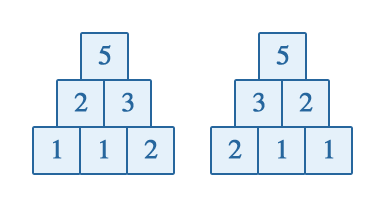 |
|
|
| 1) | |
| | | Returns: 1 | The only number pyramid with base of size 5 and 16 at the top looks like this:
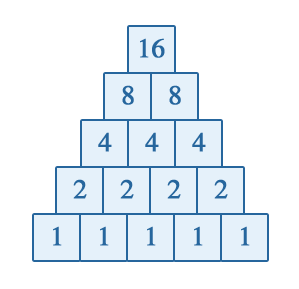 |
|
|
| 2) | |
| | |
| 3) | |
| | |
| 4) | |
| | |

