Problem Statement |
| | John and Brus are interested in a new game called "Hexagon Flower". The rules are simple. You are given a flower formed by seven hexagons arranged as follows:
The objective of the game is to place a number in each hexagon of the flower such that all of the following conditions are satisfied:
- Each number is an integer between 1 and n, inclusive.
- Each number is distinct.
- For every pair of adjacent hexagons, if the numbers placed in them are a and b, then a%k != b%k.
Given n and k, return the total number of distinct solutions. Two solutions are considered the same if you can rotate one to form the other.
For example, if n = 8 and k = 4, then:
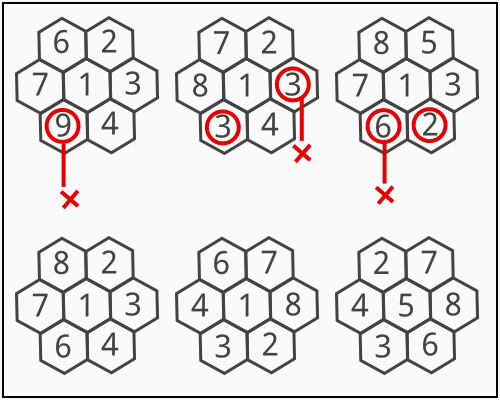
The top three placements are not valid. The other three placements are valid, but the first two among them are considered equal since one can be rotated to become the other. |
| |
Definition |
| | | Class: | TheHexagonsDivTwo | | Method: | count | | Parameters: | int, int | | Returns: | long | | Method signature: | long count(int n, int k) | | (be sure your method is public) |
|
| |
|
| |
Constraints |
| - | n will be between 1 and 300, inclusive. |
| - | k will be between between 1 and 9, inclusive. |
| |
Examples |
| 0) | |
| | | Returns: 0 | | There is no way to place all 7 numbers (1 through 7, inclusive) such that no two adjacent numbers are equal modulo 3. |
|
|
| 1) | |
| | |
| 2) | |
| | |
| 3) | |
| | |

